题目内容
7.下列选项中,说法正确的个数是( )(1)命题“?x0∈R,${x_0}^2-{x_0}≤0$”的否定为“?x∈R,x2-x>0”;
(2)命题“在△ABC中,A>30°,则$sinA>\frac{1}{2}$”的逆否命题为真命题;
(3)设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的充分必要条件;
(4)若统计数据x1,x2,…,xn的方差为1,则2x1,2x2,…,2xn的方差为2;
(5)若两个随机变量的线性相关性越强,则相关系数绝对值越接近1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 (1),根据含有量词的命题的否定判断;
(2),根据命题的逆否命题与原命题同真假命题;
(3),根据充分条件和必要条件的定义判断.;
(4)由公式D(ax+b)=a2D(X) 可求出2x1,2x2,…,2xn的方差;
(5)利用两个随机变量的线性相关性强弱与相关系数的绝对值的关系即可判断出正误;.
解答 解:对于(1),命题“?x0∈R,${x_0}^2-{x_0}≤0$”的否定为“?x0∈R,x02-x0>0”,故错;
对于(2),命题“在△ABC中,A>30°,则$sinA>\frac{1}{2}$”是假命题,其逆否命题与原命题同真假命题,故错;
对于(3),设{an}是公比为q的等比数列,当q>1且a1>0才是“{an}为递增数列”的充分必要条件,故错;
对于(4)由公式D(ax+b)=a2D(X) 德,若统计数据x1,x2,…,xn的方差为1,则2x1,2x2,…,2xn的方差为4,故错;
对于(5,)若两个随机变量的线性相关性越强,则相关系数绝对值越接近1,正确.
故选:A.
点评 本题主要考查命题的真假判断,解决的关键是对于命题的否定以及真值的判定的运用,属于基础题

练习册系列答案
相关题目
17.设点A(3,-5),B(-2,-2),直线l过点P(1,1)且与线段AB相交,则直线l的斜率k的取值范围是( )
| A. | k≥1或k≤-3 | B. | -3≤k≤1 | C. | -1≤k≤3 | D. | 以上都不对 |
15.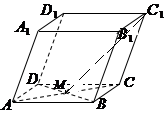 四棱柱ABCD-A1B1C1D1的底面是平行四边形,M是AC与BD的交点.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,则$\overrightarrow{{C_1}M}$可以表示为( )
四棱柱ABCD-A1B1C1D1的底面是平行四边形,M是AC与BD的交点.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,则$\overrightarrow{{C_1}M}$可以表示为( )
 四棱柱ABCD-A1B1C1D1的底面是平行四边形,M是AC与BD的交点.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,则$\overrightarrow{{C_1}M}$可以表示为( )
四棱柱ABCD-A1B1C1D1的底面是平行四边形,M是AC与BD的交点.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,则$\overrightarrow{{C_1}M}$可以表示为( )| A. | $\overrightarrow a+\overrightarrow b+\frac{1}{2}\overrightarrow c$ | B. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ | C. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b-\overrightarrow c$ | D. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ |
2.3<m<5是方程$\frac{{x}^{2}}{5-m}$+$\frac{{y}^{2}}{m-3}$=1表示椭圆的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.已知全集U={0,2,4,6,8,10},集合A={2,4,6},B={1},则(∁UA)∪B等于( )
| A. | {0,1,8,10} | B. | {1,2,4,6} | C. | {0,8,10} | D. | ∅ |