题目内容
已知函数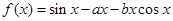
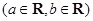 .
.
(1)若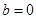 ,讨论函数
,讨论函数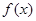 在区间
在区间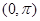 上的单调性;
上的单调性;
(2)若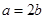 且
且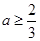 ,对任意的
,对任意的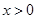 ,试比较
,试比较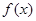 与
与 的大小.
的大小.
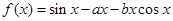
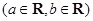 .
.(1)若
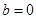 ,讨论函数
,讨论函数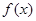 在区间
在区间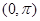 上的单调性;
上的单调性;(2)若
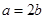 且
且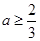 ,对任意的
,对任意的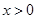 ,试比较
,试比较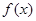 与
与 的大小.
的大小.(1)参考解析;(2)

试题分析:(1)函数
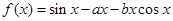
 ,
,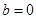 ,所以可得函数
,所以可得函数 .通过对函数求导,以及对
.通过对函数求导,以及对 讨论即可得到结论.
讨论即可得到结论.(2)由
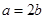 且对任意的
且对任意的 ,将
,将 换留下
换留下 一个参数,又
一个参数,又 恒成立.构建新函数
恒成立.构建新函数 ,通过对函数求导得到
,通过对函数求导得到 ,对
,对 的取值分类讨论即可得结论.
的取值分类讨论即可得结论.试题解析:(1)
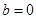 时,
时, ,则
,则 , 1分
, 1分当
 时,
时, ,所以函数
,所以函数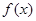 在区间
在区间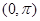 上单调递减; 2分
上单调递减; 2分当
 时,
时, ,所以函数
,所以函数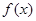 在区间
在区间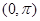 上单调递增; 3分
上单调递增; 3分当
 时,存在
时,存在 ,使得
,使得 ,即
,即 , 4分
, 4分 时,
时, ,函数
,函数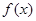 在区间
在区间 上单调递增, 5分
上单调递增, 5分 时,
时, ,函数
,函数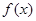 在区间
在区间 上单调递减. 6分
上单调递减. 6分(2)
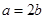 时,
时, ,猜测
,猜测 恒成立, 7分
恒成立, 7分证明:
 等价于
等价于 ,
,记
 ,则
,则 , 10分
, 10分当
 ,即
,即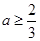 时,
时, ,
, 在区间
在区间 上单调递减, 12分
上单调递减, 12分所以当
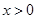 时,
时, ,即
,即 恒成立; 14分
恒成立; 14分
练习册系列答案
相关题目
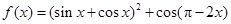 .
. 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;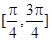 上的取值范围.
上的取值范围.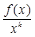 在
在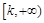 上为增函数,则称
上为增函数,则称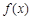 为“k次比增函数”,其中
为“k次比增函数”,其中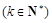 . 已知
. 已知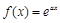 其中e为自然对数的底数.
其中e为自然对数的底数.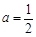 时,求函数
时,求函数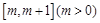 在
在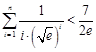 .
.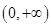 的单调函数
的单调函数 ,对任意的
,对任意的 ,都有
,都有 ,若
,若 是方程
是方程 的一个解,则
的一个解,则


 上是减函数的是( )
上是减函数的是( )



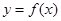 对任意的
对任意的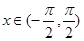 满足
满足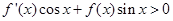 (其中
(其中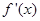 是函数
是函数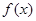 的导函数),则下列不等式成立的是( )
的导函数),则下列不等式成立的是( )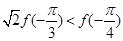
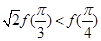
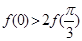
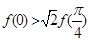
 ,当扇形的周长最小时,扇形的中心角
,当扇形的周长最小时,扇形的中心角
 为( )
为( )

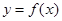 在
在 上为偶函数,当
上为偶函数,当 时,
时,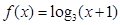 ,若
,若 ,则实数
,则实数 的取值范围是
的取值范围是