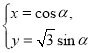题目内容
【题目】已知定义在![]() 上的函数
上的函数![]() 满足:①对任意实数
满足:①对任意实数![]() ,
,![]() ,都有
,都有![]() ;②对任意
;②对任意![]() ,都有
,都有![]() .
.
(1)求![]() ,并证明
,并证明![]() 是
是![]() 上的单调增函数;
上的单调增函数;
(2)若![]()
![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)已知![]() ,方程
,方程![]() 有三个根
有三个根![]() ,若
,若![]() ,求实数
,求实数![]() .
.
【答案】(1)![]() ,证明见详解;(2)
,证明见详解;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)对抽象函数进行赋值,令![]() ,
,![]() ,即可求得
,即可求得![]() ;根据单调性的定义,作差,比较大小,定号即可证明;需要注意抽象函数在作差时的变形;
;根据单调性的定义,作差,比较大小,定号即可证明;需要注意抽象函数在作差时的变形;
(2)利用函数的单调性,将问题转化为绝对值不等式恒成立的问题,再利用绝对值三角不等式求得最值,即可得到![]() 的取值范围.
的取值范围.
(3)构造函数![]() ,从而将问题转化为函数图像交点的问题,数形结合,再利用
,从而将问题转化为函数图像交点的问题,数形结合,再利用![]() ,即可求解.
,即可求解.
(1)令![]() ,
,![]() ,则代入条件①,
,则代入条件①,
得:![]() 又
又![]() ,则
,则![]() ;
;
设![]() ,则
,则![]()
![]() ,
,
因为任意![]() ,都有
,都有![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() 且
且![]() ,都有
,都有![]() ,
,
则对任意![]() 都有
都有![]()
则![]() ,所以
,所以![]() ,
,
所以:![]() 是
是![]() 上的单调增函数.
上的单调增函数.
(2)由条件![]()
![]() 恒成立;
恒成立;
可化为![]() ,
,
即:![]() ,
,
即![]() 对
对![]() 恒成立.
恒成立.
因![]() ,
,
故只需![]() .
.
解得![]() .
.
(3)设![]() ,显然
,显然![]() ,
,
∴![]() ,
,
方程![]() 等价于
等价于
![]() 即:
即:![]() ,
,
∵![]() 且
且![]() 可改写为:
可改写为: ,
,
由![]() ,
,
又当![]() 时,
时,![]() ,
,
∴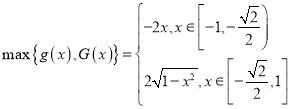 ,画出函数图像如下所示:
,画出函数图像如下所示:
于是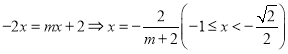 ,∴
,∴![]() ,
,
由![]() 或
或![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,
由已知条件![]() ,∴
,∴![]() ,
,
即![]() ,
,
又![]() ,
,
∴![]() .
.

【题目】某工厂共有男女员工500人,现从中抽取100位员工对他们每月完成合格产品的件数统计如下:
每月完成合格产品的件数(单位:百件) |
|
|
|
|
|
频数 | 10 | 45 | 35 | 6 | 4 |
男员工人数 | 7 | 23 | 18 | 1 | 1 |
(1)其中每月完成合格产品的件数不少于3200件的员工被评为“生产能手”.由以上统计数据填写下面![]() 列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
非“生产能手” | “生产能手” | 合计 | |
男员工 | |||
女员工 | |||
合计 |
(2)为提高员工劳动的积极性,工厂实行累进计件工资制:规定每月完成合格产品的件数在定额2600件以内的,计件单价为1元;超出![]() 件的部分,累进计件单价为1.2元;超出
件的部分,累进计件单价为1.2元;超出![]() 件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
附:![]() ,
,
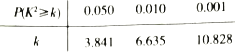 .
.