题目内容
将边长为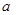 米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?
米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?
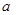 米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?
米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?V(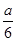 )=
)=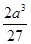 , 即为容积的最大值,此时小正方形的边长为
, 即为容积的最大值,此时小正方形的边长为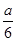 .
.
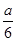 )=
)=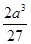 , 即为容积的最大值,此时小正方形的边长为
, 即为容积的最大值,此时小正方形的边长为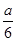 .
. 试题分析:设小正方形的边长为x,则盒底的边长为a-2x,
∴方盒的体积
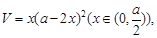 4分
4分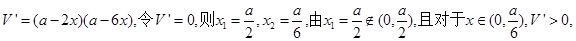
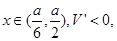 10分
10分∴函数V在点x=
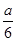 处取得极大值,由于问题的最大值存在,
处取得极大值,由于问题的最大值存在,∴V(
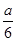 )=
)=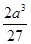 , 即为容积的最大值,此时小正方形的边长为
, 即为容积的最大值,此时小正方形的边长为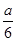 . 12分
. 12分点评:中档题,作为应用问题,往往涉及确定函数的最值。求最值的方法有,不等式法、导数法等。实际问题中,当驻点个数只有一个时,其既是极值点也是最值点。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
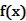 满足
满足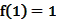 ,且
,且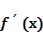 在R上恒有
在R上恒有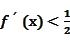 ,则不等式
,则不等式 的解集为 _______________
的解集为 _______________
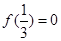 ,则不等式
,则不等式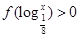 的解集是
的解集是  ,则对于不同的实数a,函数
,则对于不同的实数a,函数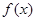 的单调区间个数不可能是( )
的单调区间个数不可能是( )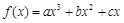 (
( )是定义在
)是定义在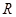 上的奇函数,且
上的奇函数,且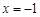 时,函数
时,函数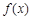 取极值1.
取极值1. ,若
,若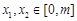 (
(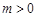 ),不等式
),不等式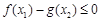 恒成立,求实数
恒成立,求实数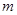 的取值范围;
的取值范围;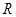 上的函数
上的函数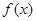 满足:
满足: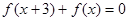 ,且函数
,且函数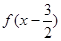 为奇函数。给出以下3个命题:
为奇函数。给出以下3个命题: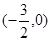 对称;
对称;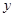 轴对称。
轴对称。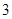
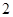
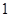

 .
. 时,求
时,求 的单调区间,如果函数
的单调区间,如果函数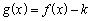 仅有两个零点,求实数
仅有两个零点,求实数 的取值范围;
的取值范围;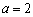 时,试比较
时,试比较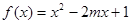 在
在 上是增函数,q:函数
上是增函数,q:函数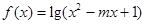 的定义域为R.
的定义域为R.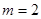 ,试判断命题p的真假;
,试判断命题p的真假; 的取值范围.
的取值范围.