Question

在椭圆上，对不同于顶点的任意三个点M，A，B，存在锐角θ，使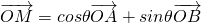．则直线OA与OB的斜率之积为________．

Answer 1

分析：设A（x₁，y₁），B（x₂，y₂），M（x，y），由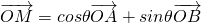，可得x，y的坐标表达式，进而根据M在椭圆上，可得直线OA与OB的斜率之积．
解答：设A（x₁，y₁），B（x₂，y₂），
则①，②．
又设M（x，y），∵，
∴
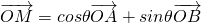∵M在椭圆上，∴+（y₁cosθ+y₂sinθ）²=1．
整理得（）cos²θ+（）sin²θ+2（+y₁y₂）cosθsinθ=1．
将①②代入上式，并注意cosθsinθ≠0，得+y₁y₂=0．
所以，k_OAk_OB==
故答案为：
点评：本题考查向量知识的运用，考查运算能力及探究能力，属于中档题．