题目内容
已知A、B是椭圆 =1(a>b>0)和双曲线
=1(a>b>0)和双曲线 =1(a>0,b>0)的公共顶点.P是双曲线上的动点,M是椭圆上的动点(P、M都异于A、B),且满足
=1(a>0,b>0)的公共顶点.P是双曲线上的动点,M是椭圆上的动点(P、M都异于A、B),且满足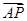 +
+ =λ(
=λ(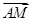 +
+ ),其中λ∈R,设直线AP、BP、AM、BM的斜率分别记为k1、k2、k3、k4,k1+k2=5,则k3+k4=________.
),其中λ∈R,设直线AP、BP、AM、BM的斜率分别记为k1、k2、k3、k4,k1+k2=5,则k3+k4=________.

 =1(a>b>0)和双曲线
=1(a>b>0)和双曲线 =1(a>0,b>0)的公共顶点.P是双曲线上的动点,M是椭圆上的动点(P、M都异于A、B),且满足
=1(a>0,b>0)的公共顶点.P是双曲线上的动点,M是椭圆上的动点(P、M都异于A、B),且满足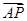 +
+ =λ(
=λ(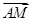 +
+ ),其中λ∈R,设直线AP、BP、AM、BM的斜率分别记为k1、k2、k3、k4,k1+k2=5,则k3+k4=________.
),其中λ∈R,设直线AP、BP、AM、BM的斜率分别记为k1、k2、k3、k4,k1+k2=5,则k3+k4=________.
-5
设P(m,n)、M(s,t),则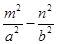 =1,m2-a2=
=1,m2-a2=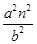 ,
,
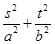 =1,s2-a2=-
=1,s2-a2=-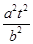 ,由
,由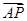 +
+ =λ(
=λ(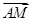 +
+ ).
).
得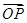 =λ
=λ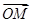 ,即
,即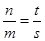 .k1+k2=
.k1+k2=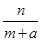 +
+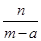 =
=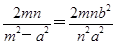 =5,∴
=5,∴
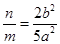 ,k3+k4=
,k3+k4=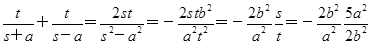 =-5.
=-5.
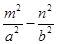 =1,m2-a2=
=1,m2-a2=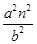 ,
,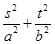 =1,s2-a2=-
=1,s2-a2=-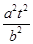 ,由
,由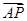 +
+ =λ(
=λ(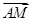 +
+ ).
).得
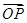 =λ
=λ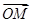 ,即
,即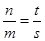 .k1+k2=
.k1+k2=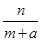 +
+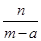 =
=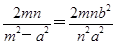 =5,∴
=5,∴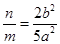 ,k3+k4=
,k3+k4=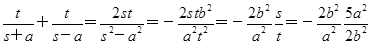 =-5.
=-5.
练习册系列答案
相关题目
 M为CD的中点.
M为CD的中点.
 ,使
,使 ,且P点到A、B 的距离和为定值,求点P的轨迹E的方程;
,且P点到A、B 的距离和为定值,求点P的轨迹E的方程; 的直线与轨迹E交于P、Q两点,求
的直线与轨迹E交于P、Q两点,求 面积的最大值.
面积的最大值.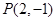 的直线
的直线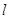 交椭圆
交椭圆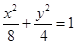 于
于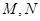 两点,
两点,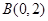 是椭圆的一个顶点,若线段
是椭圆的一个顶点,若线段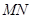 的中点恰为点
的中点恰为点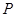 .
.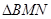 的面积.
的面积. +
+
 的轨迹C2的方程.
的轨迹C2的方程.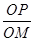 =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线.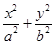 =1(a>b>0)的上,下两个顶点为A,B,直线l:y=-2,点P是椭圆上异于点A,B的任意一点,连接AP并延长交直线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为k1,BP所在的直线的斜率为k2.若椭圆的离心率为
=1(a>b>0)的上,下两个顶点为A,B,直线l:y=-2,点P是椭圆上异于点A,B的任意一点,连接AP并延长交直线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为k1,BP所在的直线的斜率为k2.若椭圆的离心率为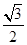 ,且过点A(0,1).
,且过点A(0,1).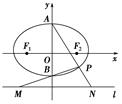
 +y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
+y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率. =2
=2 ,求直线AB的方程.
,求直线AB的方程. 上一点,F1、F2为椭圆的左、右焦点,B为椭圆右顶点,若
上一点,F1、F2为椭圆的左、右焦点,B为椭圆右顶点,若 平分线与
平分线与 的平分线交于点
的平分线交于点 ,则
,则 .
.