题目内容
11.已知函数f(x)=3sin(2x-$\frac{π}{6}$).(1)求函数f(x)的最小正周期、最小值;
(2)求函数f(x)图象的对称中心;
(3)求函数f(x)的单调递增区间.
分析 利用正弦函数的图象性质,即可得出结论.
解答 解:(1)最小正周期T=π …(2分)
当2x-$\frac{π}{6}$=-$\frac{π}{2}$+2kπ(k∈Z)时,f(x)有最小值-3 …(4分)
(2)令2x-$\frac{π}{6}$=kπ(k∈Z),则x=$\frac{π}{12}+\frac{kπ}{2}$…(6分)
所以函数f(x)图象的对称中心为($\frac{π}{12}+\frac{kπ}{2}$,0)(k∈Z),…(8分)
(3)令-$\frac{π}{2}$+2kπ≥2x-$\frac{π}{6}$≤$\frac{π}{2}$+2kπ(…(10分)
则-$\frac{π}{6}$+kπ≤x≤$\frac{π}{3}$+kπ
所以函数f(x)的单调递增区间为[-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z)…(12分)
点评 本题考查正弦函数的图象性质,考查学生的计算能力,属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
16.抛物线x=2y2的准线方程是( )
| A. | y=-$\frac{1}{2}$ | B. | x=-$\frac{1}{8}$ | C. | y=$\frac{1}{2}$ | D. | x=$\frac{1}{8}$ |
20.已知递增的等比数列{an}中,a1,a2,a3分别为下表中第一、二、三行中某一个数,且a1,a2,a3中的任何两个数不在下表中同一行和同一列,
(1)求数列{an}通项公式;
(2)若数列{bn}满足${b_n}={a_n}+{(-1)^n}ln{a_n}$,若n为偶数,求数列{bn}的前n项和.
| 第一列 | 第二列 | 第三列 | |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 6 | 4 | 14 |
| 第三行 | 9 | 8 | 18 |
(2)若数列{bn}满足${b_n}={a_n}+{(-1)^n}ln{a_n}$,若n为偶数,求数列{bn}的前n项和.
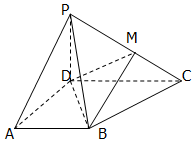 如图,四棱锥P-ABCD中,底面ABCD为梯形,∠DAB=60°,AB∥CD,AD=CD=2AB=2,PD⊥底面ABCD,M为PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为梯形,∠DAB=60°,AB∥CD,AD=CD=2AB=2,PD⊥底面ABCD,M为PC的中点. 已知an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记S(m,n)表示该数阵中第m行中从左到右的第n个数,则S(8,6)=( )
已知an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记S(m,n)表示该数阵中第m行中从左到右的第n个数,则S(8,6)=( )