题目内容
 ,其中ω>0,且f(x)的图象在y轴右侧第一个最高点的横坐标为
,其中ω>0,且f(x)的图象在y轴右侧第一个最高点的横坐标为 ,
,
(Ⅰ)求f(x)的解析式;
(Ⅱ)写出f(x)的单调递减区间(只写结果不用写出步骤);
(Ⅲ)由y=sinx的图象,经过怎样的变换,可以得到f(x)的图象?
解:(Ⅰ). =
= (1分)
(1分)
= (2分)
(2分)
∵f(x)的图象在y轴右侧第一个最高点的横坐标为
∴ ,解得
,解得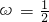 (3分)
(3分)
∴ (4分)
(4分)
(Ⅱ).f(x)的单减区间是 (8分)
(8分)
(Ⅲ)将y=sinx向左平移 个单位,纵坐标不变;(10分)
个单位,纵坐标不变;(10分)
再向上平移 个单位,横坐标不变,就得到f(x)的图象.(12分).
个单位,横坐标不变,就得到f(x)的图象.(12分).
分析:(Ⅰ)利用二倍角公式、两角和的正弦函数化简函数的表达式,通过f(x)的图象在y轴右侧第一个最高点的横坐标为 ,求出ω,然后求f(x)的解析式;
,求出ω,然后求f(x)的解析式;
(Ⅱ)直接通过正弦函数的单调减区间,写出f(x)的单调递减区间(只写结果不用写出步骤);
(Ⅲ)由y=sinx的图象,向左平移 个单位,纵坐标不变;再向上平移
个单位,纵坐标不变;再向上平移 个单位,横坐标不变,就得到f(x)的图象.
个单位,横坐标不变,就得到f(x)的图象.
点评:本题是中档题,考查三角函数的化简求值,函数解析式的求法,函数图象的平行,考查计算能力.
 =
= (1分)
(1分)=
 (2分)
(2分)∵f(x)的图象在y轴右侧第一个最高点的横坐标为

∴
 ,解得
,解得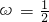 (3分)
(3分)∴
 (4分)
(4分)(Ⅱ).f(x)的单减区间是
 (8分)
(8分)(Ⅲ)将y=sinx向左平移
 个单位,纵坐标不变;(10分)
个单位,纵坐标不变;(10分)再向上平移
 个单位,横坐标不变,就得到f(x)的图象.(12分).
个单位,横坐标不变,就得到f(x)的图象.(12分).分析:(Ⅰ)利用二倍角公式、两角和的正弦函数化简函数的表达式,通过f(x)的图象在y轴右侧第一个最高点的横坐标为
 ,求出ω,然后求f(x)的解析式;
,求出ω,然后求f(x)的解析式;(Ⅱ)直接通过正弦函数的单调减区间,写出f(x)的单调递减区间(只写结果不用写出步骤);
(Ⅲ)由y=sinx的图象,向左平移
 个单位,纵坐标不变;再向上平移
个单位,纵坐标不变;再向上平移 个单位,横坐标不变,就得到f(x)的图象.
个单位,横坐标不变,就得到f(x)的图象.点评:本题是中档题,考查三角函数的化简求值,函数解析式的求法,函数图象的平行,考查计算能力.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
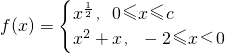 ,其中c>0.且f(x)的值域是[-
,其中c>0.且f(x)的值域是[- ,2],则c的取值范围是________.
,2],则c的取值范围是________.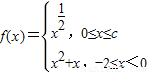 ,其中c>0.且f(x)的值域是[-
,其中c>0.且f(x)的值域是[- ,2],则c的取值范围是 .
,2],则c的取值范围是 .