题目内容
（本小题12分）已知数列
是等差数列，
；数列
的前n项和是
，且
．
（Ⅰ）求数列的通项公式；
（II）求证：数列是等比数列；
（Ⅲ）记
，求
的前n项和
．
【答案】
（Ⅰ）
（II）略
（Ⅲ）
【解析】解：（Ⅰ）设
的公差为
，则：
，
，
∵
，
，∴
，∴
． ……………………2分
∴．
……………………4分
（II）当
时，
，由
，得
．
……………………5分
当
时，
，
，
∴
，即
．
…………………………7分
∴
．
∴
是以
为首项，
为公比的等比数列．
………………………8分
（Ⅲ）由（2）可知：
．
………………………9分
∴
．
…………………10分
∴
．
∴
．
∴
． …………………………13分
∴．
…………………………14分
练习册系列答案
相关题目
，
，直线
与函数
、
的k*s#5^u图象都相切，且与函数
.
的k*s#5^u值；
(其中
是
的k*s#5^u最大值；
时，求证：
.
中，
。
中，
，求数列
项和
.
轴上的抛物线与直线
交于P、Q两点，|PQ|=
，求抛物线的方程
；
过
且与圆C相切，求直线
，使直线
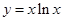
处的切线方程。