题目内容
△ABC中,内角A,B,C的对边分别是a,b,c,已知a,b,c成等差数列,且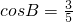 .
.
(1)求cosAcosC的值;
(2)求tanA+tanC值.
(3)判断等式 有无成立的可能?如果有,求出a,b,c的一组值;如果没有,说明理由.
有无成立的可能?如果有,求出a,b,c的一组值;如果没有,说明理由.
解:(1)∵a,b,c成等差数列,∴2b=a+c
∵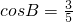 ,∴
,∴ ,
,
∴取特殊值a=3,b=4,c=5,
∴ ,
,
cosAcosC=0.
(2)tanA+tanC=
=
= .(7分)
.(7分)
(3) 不可能成立.取AC中点O,连接BO
不可能成立.取AC中点O,连接BO
∵ ,若
,若 ,
,
∴BO⊥AC(9分)
从而 ,即a=c,
,即a=c,
又∵b2=ac∴a=b=c∴
∴ ,与已知
,与已知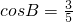 矛盾,
矛盾,
∴ 不可能成立.(14分)
不可能成立.(14分)
分析:(1)由a,b,c成等差数列,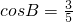 ,取特殊值a=3,b=4,c=5,故
,取特殊值a=3,b=4,c=5,故 ,cosAcosC=0.
,cosAcosC=0.
(2)tanA+tanC= =
= .
.
(3) 不可能成立.取AC中点O,连接BO,由题设能导出
不可能成立.取AC中点O,连接BO,由题设能导出 ,与已知
,与已知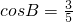 矛盾,所以
矛盾,所以 不可能成立.
不可能成立.
点评:本题考查数列的性质和应用,解题时要认真审题,注意三角函数性质和公式的灵活运用.
∵
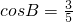 ,∴
,∴ ,
,∴取特殊值a=3,b=4,c=5,
∴
 ,
,cosAcosC=0.
(2)tanA+tanC=

=

=
 .(7分)
.(7分)(3)
 不可能成立.取AC中点O,连接BO
不可能成立.取AC中点O,连接BO∵
 ,若
,若 ,
,∴BO⊥AC(9分)
从而
 ,即a=c,
,即a=c,又∵b2=ac∴a=b=c∴

∴
 ,与已知
,与已知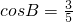 矛盾,
矛盾,∴
 不可能成立.(14分)
不可能成立.(14分)分析:(1)由a,b,c成等差数列,
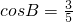 ,取特殊值a=3,b=4,c=5,故
,取特殊值a=3,b=4,c=5,故 ,cosAcosC=0.
,cosAcosC=0.(2)tanA+tanC=
 =
= .
.(3)
 不可能成立.取AC中点O,连接BO,由题设能导出
不可能成立.取AC中点O,连接BO,由题设能导出 ,与已知
,与已知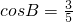 矛盾,所以
矛盾,所以 不可能成立.
不可能成立.点评:本题考查数列的性质和应用,解题时要认真审题,注意三角函数性质和公式的灵活运用.

练习册系列答案
相关题目