题目内容
将4封信投入3个邮箱,则不同的投法为 ( )
| A.81 种 | B.64 种 | C.4 种 | D.24种 |
A
解析试题分析:将4封信投入3个邮箱,每一封信都有3种不同的投法,所以不同的投法共有 .
.
考点:本小题主要考查分步乘法计数原理的应用.
点评:两个原理是解决一切计数问题的基础,关键是搞清楚是分类还是分步还有既有分类又有分步.

练习册系列答案
相关题目
将3个不同的小球放入4个盒子中,则不同放法种数有( )
| A.81 | B.64 | C.2 | D.14 |
有5个不同的小球,装入4个不同的盒内,每盒至少装一个球,共有( )不同的装法.
| A.240 | B.120 | C.600 | D.360 |
用数字1,2,3,4,5可以组成没有重复数字的五位偶数共有( )
| A.48个 | B.36个 | C.24个 | D.18个 |
从 台甲型和
台甲型和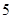 台乙型电视机中任意取出
台乙型电视机中任意取出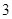 台,其中至少有甲型与乙型电视机各
台,其中至少有甲型与乙型电视机各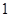 台,则不同的取法共有( )
台,则不同的取法共有( )
A.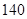 种 种 | B.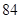 种 种 | C. 种 种 | D.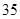 种 种 |
如图所示是某个区域的街道示意图(每个小矩形的边表示街道),则从A到B的最短线路有( )条
| A.24 | B.60 | C.84 | D.120 |
从数字1,2,3,…,10中,按由小到大的顺序取出 且
且 ,则不同的取法有( )
,则不同的取法有( )
| A.20种 | B.35种 | C.56种 | D.60种 |
 种
种  种
种  种
种  种
种  是
是 (n≥2且n∈N)的展开式中x的一次项的系数,则
(n≥2且n∈N)的展开式中x的一次项的系数,则 的值为( )
的值为( )