题目内容
设数列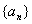 的通项是关于x的不等式
的通项是关于x的不等式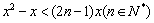 的解集中整数的个数.
的解集中整数的个数.
(Ⅰ)求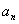 ,并且证明
,并且证明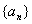 是等差数列;
是等差数列;
(Ⅱ)设m、k、p∈N*,m+p=2k,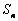 为
为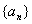 的前n项和.求证:
的前n项和.求证: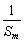 +
+ ≥
≥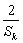 ;
;
(Ⅲ)对于(Ⅱ)中的命题,对一般的各项均为正数的等差数列还成立吗?如果成立,请证明你的结论;如果不成立,请说明理由.
【答案】
(Ⅰ)由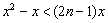 得
得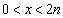 ,其中整数有2n-1个,故
,其中整数有2n-1个,故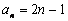 ,
,
又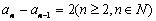 ,所以数列
,所以数列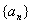 是等差数列…………(6分)
是等差数列…………(6分)
(Ⅱ)由(Ⅰ)知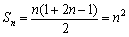 ,∴ Sm=m2,Sp=p2,Sk=k2.
,∴ Sm=m2,Sp=p2,Sk=k2.
由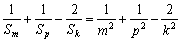
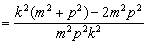 w≥
w≥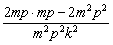 =0,
=0,
即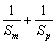 ≥
≥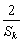 .…………………(12分)
.…………………(12分)
(Ⅲ)结论成立,证明如下:设等差数列{an}的首项为a1,公差为d,
则 ,
,
∵ 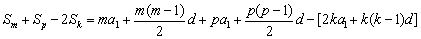
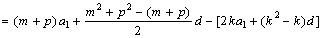 ,
,
把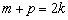 代入上式化简得
代入上式化简得
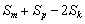 =
=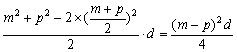 ≥0,∴ Sm+Sp≥2Sk .
≥0,∴ Sm+Sp≥2Sk .
又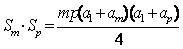 =
=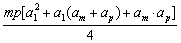
≤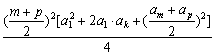
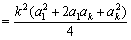
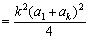
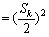 ,
,
∴ 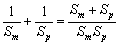 ≥
≥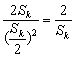 .故原不等式得证.…………(16分)
.故原不等式得证.…………(16分)

练习册系列答案
相关题目
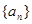 的通项是关于x的不等式
的通项是关于x的不等式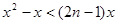
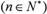 的解集中整数的个数.
的解集中整数的个数.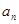 并且证明
并且证明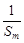 +
+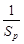 ≥
≥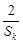 ;
;