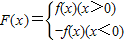Question

已知在f（x）=（x+1）ⁿ的展开式中，只有第6项的二项式系数最大．
（1）求n；
（2）求f（96）被10除所得的余数．

Answer 1

分析：（1）利用二项式系数的性质可知第6项为展开式的中间项，从而可知n的值；
（2）由于f（96）=（96+1）¹⁰=（100-3）¹⁰，利用二项式定理可知，f（96）被10除得的余数与3¹⁰除得的余数相同，从而可求答案．

解答：解：（1）∵f（x）=（x+1）ⁿ的展开式中，只有第6项的二项式系数最大，
∴

n

2

+1=6，
∴n=10…（4分）
（2）∵f（96）=（96+1）¹⁰=97¹⁰=（100-3）¹⁰
=

C

0 10

×100¹⁰-

C

1 10

×100⁹×3+

C

2 10

×100⁸×3²-…-

C

9 10

×100×3⁹+

C

10 10

•3¹⁰
∴f（96）被10除得的余数与3¹⁰除得的余数相同…（10分）
又3¹⁰=9⁵=（10-1）⁵=

C

0 5

×10⁵-

C

1 5

×10⁴+

C

2 5

×10³-

C

3 5

×10²+

C

4 5

×10¹-

C

5 5

∴3¹⁰被10除得的余数为9，
∴f（96）被10除得的余数为9…（14分）

点评：本题考查二项式定理的应用，考查二项式系数的性质，突出考查整除问题，得到f（96）被10除得的余数与3¹⁰除得的余数相同是关键，属于中档题．