题目内容
 在△ABC中,∠ACB=90°,∠BAC=30°,AB=4,D、E分别为AB、AC上的点,AB⊥DE,沿DE将△ADE折起,使得平面ADE⊥平面BDEC,设AD=x.
在△ABC中,∠ACB=90°,∠BAC=30°,AB=4,D、E分别为AB、AC上的点,AB⊥DE,沿DE将△ADE折起,使得平面ADE⊥平面BDEC,设AD=x.(1)若侧视图方向为
. | DB |
(2)试将四棱锥A-BCED的体积u(x)用x表示出来.
(3)当x为何值时,u(x)取最大值.
分析:(1)侧视图方向为
,求出BC在DE上的射影的长度,即可求出侧视图面积.
(2)将四棱锥的体积转化为:SA-BCED=S△ABC-S△ADE,即可u(x)用x表示出来.
(3)利用函数的导数,通过函数的单调性,求出u(x)取最大值.
. |
| DB |
(2)将四棱锥的体积转化为:SA-BCED=S△ABC-S△ADE,即可u(x)用x表示出来.
(3)利用函数的导数,通过函数的单调性,求出u(x)取最大值.
解答: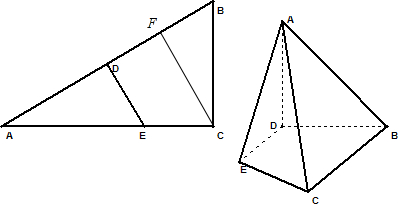 解:(1)BC在DE上的射影的长度CF=
解:(1)BC在DE上的射影的长度CF=
,几何体的左视图为三角形,高为AD=x,所以左视图的面积为:S侧=
.
(2)∵△ADE∽△ABC,
⇒
=
⇒DE=
x,∴SA-BCED=S△ABC-S△ADE=2
-
x2,
u(x)=
SDECB•AD=
(12x-x3),0<x<3.
(3)由(1)得u′(x)=
(4-x2),0<x<3,
∵?x∈(0,2),u′(x)>0,u′(2)=0,?x∈(2,3),u′(x)<0,
∴umax(x)=u(2)=
.
 解:(1)BC在DE上的射影的长度CF=
解:(1)BC在DE上的射影的长度CF=| 3 |
| ||
| 2 |
(2)∵△ADE∽△ABC,
⇒
| x | ||
2
|
| DE |
| 2 |
| ||
| 3 |
| 3 |
| ||
| 6 |
u(x)=
| 1 |
| 3 |
| ||
| 18 |
(3)由(1)得u′(x)=
3
| ||
| 18 |
∵?x∈(0,2),u′(x)>0,u′(2)=0,?x∈(2,3),u′(x)<0,
∴umax(x)=u(2)=
8
| ||
| 9 |
点评:本题考查几何体的直观图与三视图的关系,几何体的体积的求法,函数的单调性的应用,考查计算能力与转化思想.

练习册系列答案
相关题目
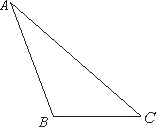 如图,在△ABC中,AC=2,BC=1,
如图,在△ABC中,AC=2,BC=1, 如图,在△ABC中,AC=BC,AB=2,O为AB的中点,沿OC将△AOC折起到△A′OC的位置,使得直线A′B与平面ABC成30°角.
如图,在△ABC中,AC=BC,AB=2,O为AB的中点,沿OC将△AOC折起到△A′OC的位置,使得直线A′B与平面ABC成30°角.