题目内容
下图是某市3月1日至14日空气质量指数趋势图,空气质量指数小于1 00表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1曰至3月1 3日中某一天到达该市,并停留2天.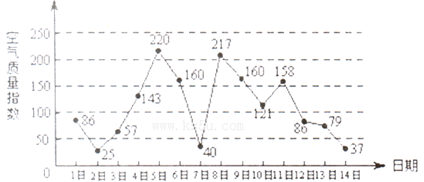
(l)求此人到达当日空气重度污染的概率;
(2)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望。
(1) ;(2)
;(2)
解析试题分析:(1)某人随机选择3月1曰至3月1 3日中某一天到达该市,有13个基本事件,由于是随机选择,每个结果出现的可能性是相等等的,而到达当天空气重度污染包含两个基本事件,故可由古典概型求其概率;
(2)此人在选择3月1曰至3月1 3日中某一天到达该市,并停留2天,有13个基本事件,它们是 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ;
;
其中两天全是优良的有: ,
, ,
, ,
, 共四个;
共四个; ;
;
两天中只有一个优良的有: ,
, ,
, ,
, 共四个;
共四个; ;
;
两天都不是优良的有5个 .
.
解:(1)重度污染有两天,故当日遇到重度污染的概率为 ;
;
(2) ;
; 是指两天内有且只有一天为优良,故到达日期只能是3日,6日,7日,11日
是指两天内有且只有一天为优良,故到达日期只能是3日,6日,7日,11日 ;
; 是指两天连续优良,故到达日期只能是1日,2日,12日,13日,
是指两天连续优良,故到达日期只能是1日,2日,12日,13日, ;
;

考点:1、古典概型;2、离散型随机变量的分布列与数学期望.

练习册系列答案
相关题目
如图,A地到火车站共有两条路径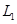 和
和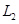 ,据统计,通过两条路径所用的时间互不影响,所用时间落在个时间段内的频率如下表:
,据统计,通过两条路径所用的时间互不影响,所用时间落在个时间段内的频率如下表: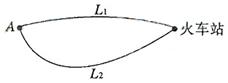
| 时间(分钟) | 10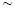 20 20 | 20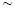 30 30 | 30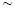 40 40 | 40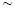 50 50 | 50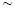 60 60 |
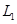 的频率 的频率 | 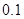 | 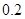 | 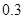 | 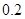 | 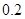 |
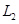 的频率 的频率 | 0 | 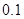 | 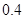 | 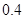 | 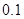 |
现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站.
(1)为了尽最大可能在各自允许的时间内赶到火车站,甲和乙应如何选择各自的路径?
(2)用X表示甲、乙两人中在允许的时间内能赶到火车站的人数,针对(1)的选择方案,求X的分布列和数学期望 .
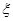 ,求
,求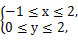 从区域W中随机取点M(x,y).
从区域W中随机取点M(x,y).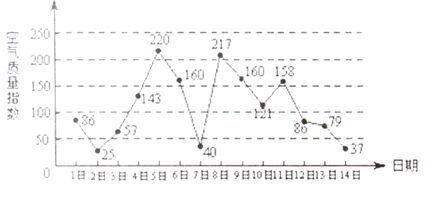
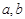 ,按以下程序进行运算:
,按以下程序进行运算: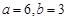 ,求程序运行后计算机输出的y的值;
,求程序运行后计算机输出的y的值;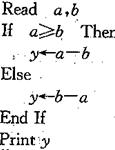
 ,
,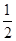 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为