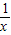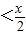Question

解下列不等式．
（I）

1

x

＜

x

2

（II）|x-1|+|x+1|＜5．

Answer 1

分析：（I）不等式

1

x

＜

x

2

，即

2-x2

2x

＜0，等价于  2x（x-

2

）（x+

2

）＞0，用穿根法求得它的解集．
（II）由绝对值的意义可得|x-1|+|x+1|表示数轴上的x到1和-1距离之和，而

5

2

和-

5

2

到1和-1距离之和正好等于5，由此可得原不等式的解集．

解答：解：（I）不等式

1

x

＜

x

2

，即

2-x2

2x

＜0，等价于 （x²-2）•2x＜0，即 2x（x-

2

）（x+

2

）＞0，
用穿根法求得它的解集为（-

2

，0）∪（

2

，+∞）．
（II）由绝对值的意义可得|x-1|+|x+1|表示数轴上的x到1和-1距离之和，而

5

2

和-

5

2

到1和-1距离之和正好等于5，
故原不等式的解集为（-

5

2

，

5

2

）．

点评：本题主要考查绝对值的意义，绝对值不等式的解法，体现了等价转化的数学思想，属于中档题．