题目内容
已知函数
（1）若
恒成立，求实数a的取值范围；
（2）若
，证明：
（1）实数a的取值范围≤1；（2）同解析；
解析:
（1）解法一：由
上恒成立.
令
在（0，1）上为减函数，在（1，+∞）上为增函数，
解法二：令
由
当
上为增函数，在（0，
）上为减函数，
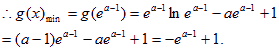
要使
在
上恒成立，
即使
恒成立，
由
（II）令
，
当
时，
练习册系列答案
教材全解字词句篇系列答案
相关题目
有极值，求b的取值范围；
处取得极值时，当
恒成立，求c的取值范围；
都有
．
在点
处的切线与圆
相切，求
的值；
时，函数
轴的上方，试求出
恒成立，求实数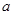
的最小值.
且关于
的方程
在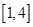
上恰有两个不相等的实数根，求实数
的取值范围；
满足：
求证：
.
，求
的值；
对于
恒成立，求实数
的取值范围。