题目内容
对于以下命题
①存在α∈(0,
),使sinα+cosα=
②存在区间(a,b)使y=cosx为减函数,且sinx<0
③y=sin(2x-
)的一条对称轴为直线x=-
④y=cos2x+sin(
-x)既有最大值、最小值,又是偶函数
⑤y=sin|2x-
|的最小正周期为
以上命题正确的有
①存在α∈(0,
| π |
| 2 |
| 4 |
| 5 |
②存在区间(a,b)使y=cosx为减函数,且sinx<0
③y=sin(2x-
| π |
| 3 |
| π |
| 12 |
④y=cos2x+sin(
| π |
| 2 |
⑤y=sin|2x-
| π |
| 6 |
| π |
| 2 |
以上命题正确的有
③④
③④
(填上所有正确命题的序号)分析:对于①根据三角函数的值域范围判断正误;②结合三角函数的图象判断是否存在(a,b),推出正误;③将x的值代入,看函数是否取最值即可,能取到最值就是函数的对称轴,直接判断正误;④化简函数表达式,求其最大值最小值,判断奇偶性;⑤根据函数的周期判断即可.
解答:解:①因为α∈(0,
),使得sinα+cosα=
sin(α+
)>1,所以①错误;
②通过正弦函数、余弦函数的图象可知,不存在区间(a,b)使y=cosx为减函数而sinx<0,②错误.
③当x=-
时,y=sin(2x-
)=-1,取得最小值,故直线x=-
是f(x)的对称轴;③正确;
④y=cos2x+sin(
-x)=cos2x+cosx;既有最大、最小值,又是偶函数,④正确.
⑤y=sin|2x-
|它不是周期函数.⑤不正确,
故答案为:③④.
| π |
| 2 |
| 2 |
| π |
| 4 |
②通过正弦函数、余弦函数的图象可知,不存在区间(a,b)使y=cosx为减函数而sinx<0,②错误.
③当x=-
| π |
| 12 |
| π |
| 3 |
| π |
| 12 |
④y=cos2x+sin(
| π |
| 2 |
⑤y=sin|2x-
| π |
| 6 |
故答案为:③④.
点评:本题考查三角函数的最值,三角函数的周期性,三角函数的单调性,考查逻辑思维推理计算能力,掌握三角函数的基本知识,是解好三角函数题目的基础,考查的知识点比较多,综合性比较强,是一道中档题;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,使
,使
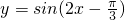 的一条对称轴为直线
的一条对称轴为直线
 既有最大值、最小值,又是偶函数
既有最大值、最小值,又是偶函数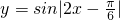 的最小正周期为
的最小正周期为
 ,使
,使
 的一条对称轴为直线
的一条对称轴为直线
 既有最大值、最小值,又是偶函数
既有最大值、最小值,又是偶函数 的最小正周期为
的最小正周期为