题目内容
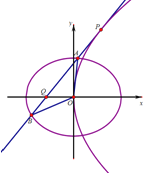
【题目】如图，椭圆
，抛物线
，过
上一点
异于原点
作的切线l交
于A，B两点，切线l交x轴于点Q．
若点P的横坐标为1，且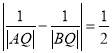
，求p的值．
求
的面积的最大值，并求证当面积取最大值时，对任意的
，直线l均与一个定椭圆相切．
【答案】（1）6；（2）
，证明见解析.
【解析】
不妨设
计算出AQ，BQ的长度代入条件计算出p值；
设
则
令
，则l：
表示出
的面积，求出其最大值，验证直线l与椭圆
相切；
解：点
，由对称性不妨设
．
于是
，于是
所以点Q是
的左焦点．
设
焦准距为
．
类比抛物线的焦半径算法可得
．
于是
，于是
，所以
．
设
于是l：
．
于是令，则l：
．
联立
．
设
，
．
．
当且仅当
取等，且满足
所以的面积的最大值为
．
注意到即为
这个等式类似于
；
于是猜想椭圆联立
得：
；
；
故当面积取最大值时，直线l均与一个定椭圆
相切．
练习册系列答案
名校课堂系列答案
相关题目
