题目内容
【题目】已知抛物线
，
为抛物线
上的点，若直线
经过点
且斜率为
，则称直线为点的“特征直线”.设
、
为方程
（
）的两个实根，记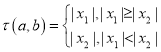
.
（1）求点
的“特征直线”的方程；
（2）已知点
在抛物线上，点的“特征直线”与双曲线
经过二、四象限的渐进线垂直，且与
轴的交于点
，点
为线段
上的点.求证：
；
（3）已知
、
是抛物线上异于原点的两个不同的点，点、的“特征直线”分别为
、
，直线、相交于点
，且与轴分别交于点
、
.求证：点
在线段
上的充要条件为
（其中
为点的横坐标）.
【答案】（1）
（2）证明见解析（3）证明见解析
【解析】
（1）计算
的斜率为1，再计算直线方程得到答案.
（2）根据与渐近线垂直得到
，线段
的方程为
，得到
，代入方程得到
，
，计算得到
.
（3））设
，
，得到
所对应的方程为：
计算得到
，分别证明充分性和必要性得到答案.
（1）由题意的斜率为1，所以点
的“特征直线”的方程为.
（2）设点
，由于双曲线
所求渐进线的斜率为
所以
，进而得，线段的方程为
所以满足
所对应方程为：
，解得，
因为
，所以
，进而
（3）设，，
则
、
的方程分别为
，
，
解、交点可得
，
，
所对应的方程为：，
必要性：因为点
在线段
上
当
时，
，得
，
当
时，
，得
，
所以
，进而
①充分性：由，得，
当时，，得，
当时，得，得，
所以点在线段上.
综上所述：点在线段上的充要条件为
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
