题目内容
设等比数列{an}的公比为q,前n项和Sn>0(n=1,2,…),求q的取值范围.
思路点拨:本题主要依据等比数列的前n项和公式将和表示出来,从而问题转化为解不等式.
解:由于数列{an}是等比数列,且Sn>0,
所以a1=S1>0,q≠0,
当q=1时,Sn=na1>0;当q≠1时,Sn=![]() >0,即
>0,即![]() >0(n=1,2,3,…),上式等价于不等式组
>0(n=1,2,3,…),上式等价于不等式组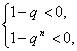 (n=1,2,3,…)①或
(n=1,2,3,…)①或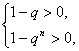 (n=1,2,3,…)②,解①得q>1;
(n=1,2,3,…)②,解①得q>1;
解②,由于n可为偶数,得-1<q<1.
综上所述,q的取值范围是(-1,0)∪(0,+∞).
[一通百通]对于等比数列的前n项和公式,在使用时要注意其公比是否为1,如果不能确定,就要针对公比是否为1而分类讨论,否则问题可能因此而漏解.

练习册系列答案
相关题目
设等比数列{an}的前n项和为Sn,若8a2+a5=0,则下列式子中数值不能确定的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设等比数列{an}的前n项和为Sn,若
=3,则
=( )
| S6 |
| S3 |
| S9 |
| S6 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |