题目内容
直线（1+4k）x-（2-3k）y+（5k+4）=0所确定的直线必经过定点 ________
（-2，1）
分析：将直线的方程转化为 k（4x+3y+5）+（x-2y+4 ）=0，定点的坐标即为
的解，解此
方程组，可得定点坐标．
解答：直线（1+4k）x-（2-3k）y+（5k+4）=0 即：k（4x+3y+5）+（x-2y+4 ）=0，
由 得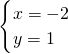 
，∴直线经过的定点坐标为（-2，1），
故答案为：（-2，1）．
点评：本题考查直线过定点问题，直线 k（ax+by+c）+（mx+ny+p）=0 一定经过两直线 ax+by+c=0和mx+ny+p=0 的交点．
分析：将直线的方程转化为 k（4x+3y+5）+（x-2y+4 ）=0，定点的坐标即为
的解，解此方程组，可得定点坐标．
解答：直线（1+4k）x-（2-3k）y+（5k+4）=0 即：k（4x+3y+5）+（x-2y+4 ）=0，
由
得 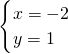，∴直线经过的定点坐标为（-2，1），故答案为：（-2，1）．
点评：本题考查直线过定点问题，直线 k（ax+by+c）+（mx+ny+p）=0 一定经过两直线 ax+by+c=0和mx+ny+p=0 的交点．
练习册系列答案
相关题目