题目内容
已知函数 ,下列命题中不正确的是
,下列命题中不正确的是
- A.f(x)的图象关于直线
 对称
对称 - B.f(x)的图象关于点
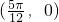 成中心对称
成中心对称 - C.f(x)在区间
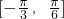 上单调递增
上单调递增 - D.f(x)在区间
 上的最大值是1,最小值是0
上的最大值是1,最小值是0
B
分析:利用两角和的正弦公式把f(x)化为 ,再利用三角函数的图象和性质即可得出.
,再利用三角函数的图象和性质即可得出.
解答:f(x)=cos2x+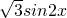 -1
-1
=
= ,
,
A.∵f( )=
)= =2×1-1=1,∴f(x)的图象关于直线
=2×1-1=1,∴f(x)的图象关于直线 对称,正确;
对称,正确;
B.∵ =
= =2sinπ-1=-1,∴f(x)的图象关于点
=2sinπ-1=-1,∴f(x)的图象关于点 成中心对称;
成中心对称;
C.由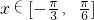 ,得
,得 ,∴
,∴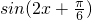 在此区间上单调递增,因此f(x)在区间
在此区间上单调递增,因此f(x)在区间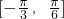 上单调递增,故正确;
上单调递增,故正确;
D.由 得
得 ,∴
,∴ ,∴
,∴ ,即0≤f(x)≤1,∴f(x)在区间
,即0≤f(x)≤1,∴f(x)在区间 上的最大值是1,最小值是0.
上的最大值是1,最小值是0.
综上可知:不正确的是B.
故选B.
点评:熟练掌握利用两角和的正弦公式把asinx+bcosx= sin(x+θ)的方法、利用三角函数的图象和性质是解题的关键.
sin(x+θ)的方法、利用三角函数的图象和性质是解题的关键.
分析:利用两角和的正弦公式把f(x)化为
 ,再利用三角函数的图象和性质即可得出.
,再利用三角函数的图象和性质即可得出.解答:f(x)=cos2x+
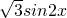 -1
-1=

=
 ,
,A.∵f(
 )=
)= =2×1-1=1,∴f(x)的图象关于直线
=2×1-1=1,∴f(x)的图象关于直线 对称,正确;
对称,正确;B.∵
 =
= =2sinπ-1=-1,∴f(x)的图象关于点
=2sinπ-1=-1,∴f(x)的图象关于点 成中心对称;
成中心对称;C.由
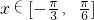 ,得
,得 ,∴
,∴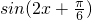 在此区间上单调递增,因此f(x)在区间
在此区间上单调递增,因此f(x)在区间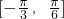 上单调递增,故正确;
上单调递增,故正确;D.由
 得
得 ,∴
,∴ ,∴
,∴ ,即0≤f(x)≤1,∴f(x)在区间
,即0≤f(x)≤1,∴f(x)在区间 上的最大值是1,最小值是0.
上的最大值是1,最小值是0.综上可知:不正确的是B.
故选B.
点评:熟练掌握利用两角和的正弦公式把asinx+bcosx=
 sin(x+θ)的方法、利用三角函数的图象和性质是解题的关键.
sin(x+θ)的方法、利用三角函数的图象和性质是解题的关键. 
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 ,下列命题中不正确的是( )
,下列命题中不正确的是( )
 的图象关于直线
的图象关于直线 对称
对称 成中心对称
成中心对称  上单调递增
上单调递增 上的最大值是
上的最大值是 ,最小值是
,最小值是
 ,下列命题中正确的是( )
,下列命题中正确的是( ) B、
B、
 D、
D、
 ,下列命题中所有正确的序号是
,下列命题中所有正确的序号是
 的定义域和值域均为
的定义域和值域均为 ;
; 单调递减,在
单调递减,在 单调递增;
单调递增; 轴对称;
轴对称; 为偶函数;
为偶函数; 则
则 或
或 .
. 幂函数的图像不过第四象限,命题
幂函数的图像不过第四象限,命题 指数函数都是增函数.则下列命题中为真命题的是(
)
指数函数都是增函数.则下列命题中为真命题的是(
) B.
B. C.
C. D.
D.