题目内容
已知数列{an}中,a1=1,且an= an-1+2n•3n-2(n≥2,n∈N?).
an-1+2n•3n-2(n≥2,n∈N?).
(1)求数列{an}的通项公式;
(2)令bn=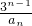 (n∈N?),数列{bn}的前n项和为Sn,试比较S2与n的大小;
(n∈N?),数列{bn}的前n项和为Sn,试比较S2与n的大小;
(3)令cn=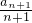 (n∈N*),数列{
(n∈N*),数列{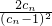 }的前n项和为Tn.求证:对任意n∈N*,都有 Tn<2.
}的前n项和为Tn.求证:对任意n∈N*,都有 Tn<2.
解:(1)由题 知,
知,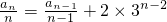 ,
,
由累加法,当n≥2时,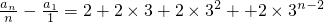
代入a1=1,得n≥2时,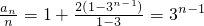
又a1=1,故an=n•3n-1(n∈N*).
(2)n∈N*时,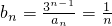 .
.
方法1:当n=1时,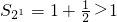 ;当n=2时,
;当n=2时,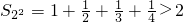 ;
;
当n=3时, .
.
猜想当n≥3时,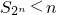 .
.
下面用数学归纳法证明:
①当n=3时,由上可知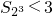 成立;
成立;
②假设:n=k(k≥3)时,上式成立,即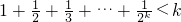 .
.
当n=k+1时,左边=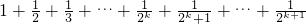
 ,
,
所以当n=k+1时成立.
由①②可知当n≥3,n∈N*时,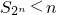 .
.
综上所述:当n=1时, ;当n=2时,
;当n=2时,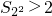 ;
;
当n≥3(n∈N*)时,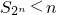 .
.
方法2: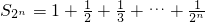
记函数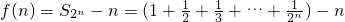
所以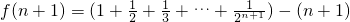
则
所以f(n+1)<f(n).
由于 ,此时
,此时 ;
;
 ,此时
,此时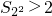 ;
;
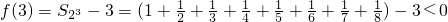 ,此时
,此时 ;
;
由于,f(n+1)<f(n),故n≥3时,f(n)≤f(3)<0,此时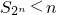 .
.
综上所述:当n=1,2时, ;当n≥3(n∈N*)时,
;当n≥3(n∈N*)时,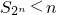 .
.
(3)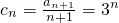
当n≥2时,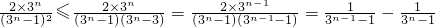
所以当n≥2时,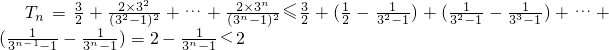 .
.
且 故对n∈N*,Tn<2得证.
故对n∈N*,Tn<2得证.
分析:第1问对条件式子两边同除以n,然后要用累加法可求出 ,从而可求出an.
,从而可求出an.
第2问有两种方法:方法1先对n=1,2,3时对 进行比较,从而猜想出一个结论,然后对这个结论用数学归纳法进行证明;
进行比较,从而猜想出一个结论,然后对这个结论用数学归纳法进行证明;
方法2把 的差构造
的差构造 ,然后利用f(n+1)-f(n)的结果正负判断出f(n)的单调性.再通过n=1,2,3时,
,然后利用f(n+1)-f(n)的结果正负判断出f(n)的单调性.再通过n=1,2,3时,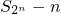 的结果变化趋势得出最后的结论.第3问先由an写出cn,然后先对
的结果变化趋势得出最后的结论.第3问先由an写出cn,然后先对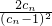 的用放缩法进行适当的放大,然后采用裂项法得出一个结果,然后再对Tn的除第一项以外的每一项按此进行放缩和裂项,运算之后很容易就看出与2的大小关系,就可以得出最后的证明结论.
的用放缩法进行适当的放大,然后采用裂项法得出一个结果,然后再对Tn的除第一项以外的每一项按此进行放缩和裂项,运算之后很容易就看出与2的大小关系,就可以得出最后的证明结论.
点评:本题第1问主要考查了用累加法求数列的通项.第2问主要考查了数学归纳证明,采用先猜想后证明的思维方式.第3问主要采用了放缩法及裂项法,难点在于放缩的把握放缩的方向和放缩的程度.总体来说第3问比较难.
 知,
知,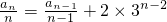 ,
,由累加法,当n≥2时,
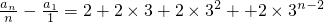
代入a1=1,得n≥2时,
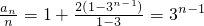
又a1=1,故an=n•3n-1(n∈N*).
(2)n∈N*时,
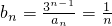 .
.方法1:当n=1时,
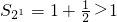 ;当n=2时,
;当n=2时,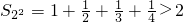 ;
;当n=3时,
 .
.猜想当n≥3时,
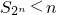 .
.下面用数学归纳法证明:
①当n=3时,由上可知
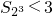 成立;
成立;②假设:n=k(k≥3)时,上式成立,即
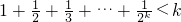 .
.当n=k+1时,左边=
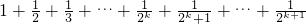
 ,
,所以当n=k+1时成立.
由①②可知当n≥3,n∈N*时,
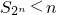 .
.综上所述:当n=1时,
 ;当n=2时,
;当n=2时,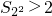 ;
;当n≥3(n∈N*)时,
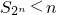 .
.方法2:
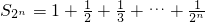
记函数
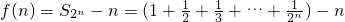
所以
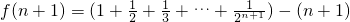
则

所以f(n+1)<f(n).
由于
 ,此时
,此时 ;
; ,此时
,此时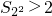 ;
;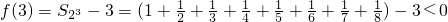 ,此时
,此时 ;
;由于,f(n+1)<f(n),故n≥3时,f(n)≤f(3)<0,此时
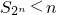 .
.综上所述:当n=1,2时,
 ;当n≥3(n∈N*)时,
;当n≥3(n∈N*)时,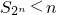 .
.(3)
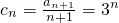
当n≥2时,
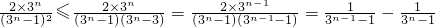
所以当n≥2时,
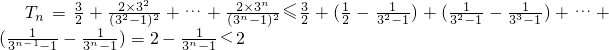 .
.且
 故对n∈N*,Tn<2得证.
故对n∈N*,Tn<2得证.分析:第1问对条件式子两边同除以n,然后要用累加法可求出
 ,从而可求出an.
,从而可求出an.第2问有两种方法:方法1先对n=1,2,3时对
 进行比较,从而猜想出一个结论,然后对这个结论用数学归纳法进行证明;
进行比较,从而猜想出一个结论,然后对这个结论用数学归纳法进行证明;方法2把
 的差构造
的差构造 ,然后利用f(n+1)-f(n)的结果正负判断出f(n)的单调性.再通过n=1,2,3时,
,然后利用f(n+1)-f(n)的结果正负判断出f(n)的单调性.再通过n=1,2,3时,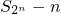 的结果变化趋势得出最后的结论.第3问先由an写出cn,然后先对
的结果变化趋势得出最后的结论.第3问先由an写出cn,然后先对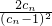 的用放缩法进行适当的放大,然后采用裂项法得出一个结果,然后再对Tn的除第一项以外的每一项按此进行放缩和裂项,运算之后很容易就看出与2的大小关系,就可以得出最后的证明结论.
的用放缩法进行适当的放大,然后采用裂项法得出一个结果,然后再对Tn的除第一项以外的每一项按此进行放缩和裂项,运算之后很容易就看出与2的大小关系,就可以得出最后的证明结论.点评:本题第1问主要考查了用累加法求数列的通项.第2问主要考查了数学归纳证明,采用先猜想后证明的思维方式.第3问主要采用了放缩法及裂项法,难点在于放缩的把握放缩的方向和放缩的程度.总体来说第3问比较难.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|