题目内容
已知在数列{an}中,a1=1,3anan-1+an-an-1=0(n≥2,n∈N+)
(Ⅰ)求证:数列 是等差数列;
是等差数列;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)若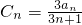 ,求数列{Cn}的前n项和Tn.
,求数列{Cn}的前n项和Tn.
解:(Ⅰ)∵a1=1,3anan-1+an-an-1=0(n≥2,n∈N+),∴3+ -
- =0,
=0,
即 -
- =3,故数列
=3,故数列 是以1为首项、以3为公差的等差数列.
是以1为首项、以3为公差的等差数列.
(Ⅱ)由(Ⅰ)知, =1+(n-1)3=3n-2,
=1+(n-1)3=3n-2,
∴an =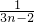 .
.
(Ⅲ)由于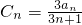 =
=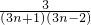 =
= -
-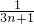 ,
,
∴数列{Cn}的前n项和Tn =(1- )+(
)+(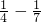 )+(
)+(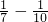 )+…+(
)+…+(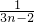 -
-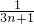 )
)
=1-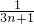 =
=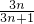 .
.
分析:(Ⅰ) 由条件可得 -
- =3,故数列
=3,故数列 是以1为首项、以3为公差的等差数列.
是以1为首项、以3为公差的等差数列.
(Ⅱ)由(Ⅰ)知, =1+(n-1)3=3n-2,从而可得数列{an}的通项公式.
=1+(n-1)3=3n-2,从而可得数列{an}的通项公式.
(Ⅲ)由于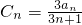 =
=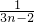 -
-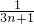 ,用裂项法求出数列{Cn}的前n项和Tn 的值.
,用裂项法求出数列{Cn}的前n项和Tn 的值.
点评:本题主要考查等比、等差关系的确定,用裂项法进行数列求和,属于中档题.
 -
- =0,
=0,即
 -
- =3,故数列
=3,故数列 是以1为首项、以3为公差的等差数列.
是以1为首项、以3为公差的等差数列.(Ⅱ)由(Ⅰ)知,
 =1+(n-1)3=3n-2,
=1+(n-1)3=3n-2,∴an =
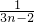 .
.(Ⅲ)由于
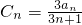 =
=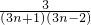 =
= -
-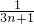 ,
,∴数列{Cn}的前n项和Tn =(1-
 )+(
)+(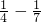 )+(
)+(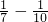 )+…+(
)+…+(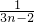 -
-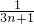 )
)=1-
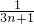 =
=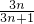 .
.分析:(Ⅰ) 由条件可得
 -
- =3,故数列
=3,故数列 是以1为首项、以3为公差的等差数列.
是以1为首项、以3为公差的等差数列.(Ⅱ)由(Ⅰ)知,
 =1+(n-1)3=3n-2,从而可得数列{an}的通项公式.
=1+(n-1)3=3n-2,从而可得数列{an}的通项公式.(Ⅲ)由于
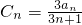 =
=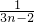 -
-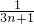 ,用裂项法求出数列{Cn}的前n项和Tn 的值.
,用裂项法求出数列{Cn}的前n项和Tn 的值.点评:本题主要考查等比、等差关系的确定,用裂项法进行数列求和,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目