题目内容
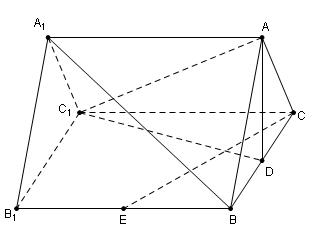
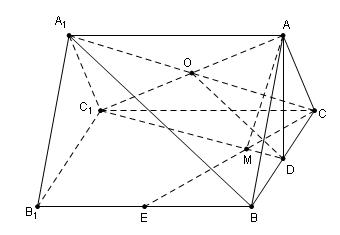
( 本小题满分12分)如图,在三棱柱
本小题满分12分)如图,在三棱柱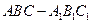 中,
中,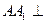 面
面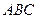 ,
,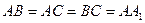 ,
,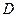 ,
,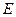 分别为
分别为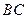 ,
,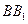
 的中点.
的中点.
(1)求证: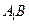 ∥平面
∥平面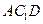 ; (2)求证:
; (2)求证: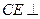 平面
平面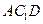 ;
;
(3)直线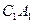 与平面
与平面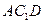 所成的角的
所成的角的 正弦值.
正弦值.
 本小题满分12分)如图,在三棱柱
本小题满分12分)如图,在三棱柱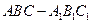 中,
中,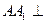 面
面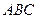 ,
,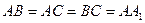 ,
,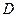 ,
,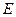 分别为
分别为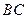 ,
,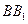
 的中点.
的中点.(1)求证:
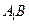 ∥平面
∥平面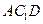 ; (2)求证:
; (2)求证: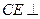 平面
平面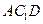 ;
;(3)直线
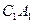 与平面
与平面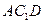 所成的角的
所成的角的 正弦值.
正弦值.
(1)证明:连结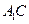 ,与
,与 交于
交于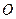 点,连结
点,连结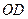 .
.
因为 ,
, 分别为
分别为 和
和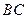 的中点, 所以
的中点, 所以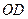 ∥
∥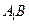 .
.
又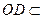 平面
平面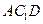 ,
,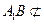 平面
平面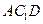 , 所以
, 所以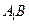 ∥平面
∥平面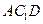 .
.
(2)证明:在直三棱柱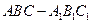 中,
中, 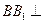 平面
平面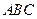 ,又
,又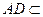 平面
平面 ,
,
所以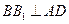 . 因为
. 因为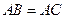 ,
,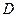 为
为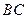 中点, 所以
中点, 所以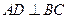 .
.
又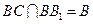 , 所以
, 所以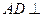 平面
平面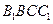 .
.
又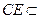 平面
平面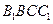 ,所以
,所以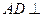
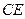 .
.
因为四边形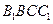 为正方形,
为正方形,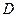 ,
,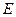 分别为
分别为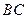 ,
,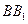 的中点,
的中点,
所以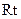 △
△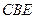 ≌
≌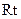 △
△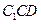 ,
,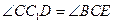 .
.
所以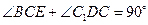 .
.
所以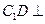
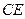 . 又
. 又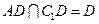 , 所以
, 所以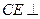 平面
平面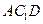 .
.
(3)设CE与C1D交于点M,连AM
由(2)知点C在面AC1D上的射影为M,故∠CAM为直线AC与面AC1D所成的角,又A1C1//AC
所以∠CAM亦为直线A1C1与面AC1D所成的角。
易求得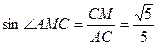
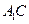 ,与
,与 交于
交于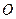 点,连结
点,连结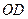 .
.
因为
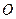 ,
,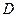 分别为
分别为 和
和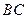 的中点, 所以
的中点, 所以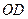 ∥
∥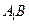 .
.又
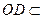 平面
平面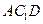 ,
,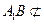 平面
平面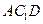 , 所以
, 所以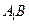 ∥平面
∥平面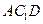 .
. (2)证明:在直三棱柱
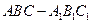 中,
中, 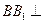 平面
平面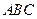 ,又
,又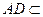 平面
平面 ,
,
所以
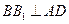 . 因为
. 因为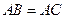 ,
,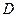 为
为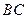 中点, 所以
中点, 所以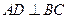 .
.又
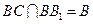 , 所以
, 所以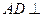 平面
平面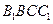 .
.又
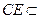 平面
平面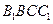 ,所以
,所以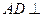
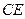 .
.因为四边形
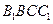 为正方形,
为正方形,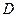 ,
,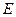 分别为
分别为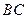 ,
,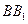 的中点,
的中点,所以
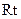 △
△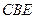 ≌
≌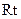 △
△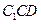 ,
,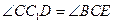 .
. 所以
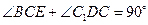 .
.所以
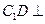
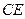 . 又
. 又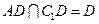 , 所以
, 所以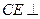 平面
平面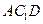 .
. (3)设CE与C1D交于点M,连AM
由(2)知点C在面AC1D上的射影为M,故∠CAM为直线AC与面AC1D所成的角,又A1C1//AC
所以∠CAM亦为直线A1C1与面AC1D所成的角。
易求得
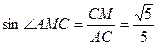
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
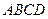 和矩形
和矩形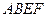 所在平面互相垂直,
所在平面互相垂直,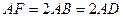 ,
,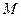 为
为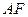 的中点,
的中点,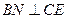 。
。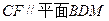 ;
; 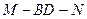 的大小
的大小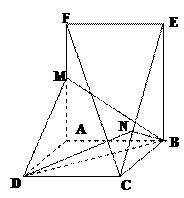
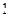
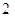

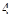
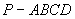 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD,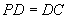 ,E是PC的中点,作
,E是PC的中点,作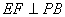 交PB于点F;
交PB于点F; 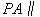 平面
平面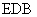 ;
; 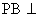 平面EFD;
平面EFD;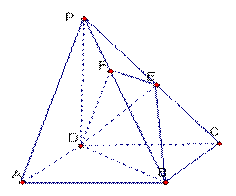
 内有一个三棱柱
内有一个三棱柱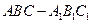 ,三棱柱的 底面为圆柱
,三棱柱的 底面为圆柱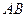 是圆
是圆 的直径。
的直径。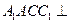 平面
平面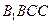 ;
;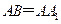 ,在圆
,在圆 柱
柱 。
。 在圆周上运动时,求
在圆周上运动时,求 与平面
与平面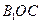 所成的角为
所成的角为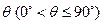 。当
。当
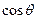 的值。
的值。

 ∠AEF=45°
∠AEF=45°
