题目内容
在△ABC中,角A、B、C的对边分别为a、b、c,若 =k (k∈R).
=k (k∈R).
(1)判 断△ABC的形状;
断△ABC的形状;
(2)若c= ,求k的值.
,求k的值.
解 (1)∵ ·
· =cbcos A,
=cbcos A, ·
· =cacos B,
=cacos B,
又 ·
· =
= ·
· ,∴bccos A=accos B,
,∴bccos A=accos B,
∴sin Bcos A=sin Acos B,
即 sin Acos B-sin Bcos A=0,∴sin(A-B)=0,
sin Acos B-sin Bcos A=0,∴sin(A-B)=0,
∵-π<A-B<π,∴A=B,即△ABC为 等腰三角形.
等腰三角形.
(2)由(1)知, ·
· =bccos A=bc·
=bccos A=bc· =k,
=k,
∵c= ,∴k=1.
,∴k=1.

练习册系列答案
相关题目
如图,在一个可以向下和向右方无限延伸的表格中,将正偶数按已填好的各个方格中的数字显现的规律填入各方格中.其中第 行,第
行,第 列的数记作
列的数记作 ,
, ,如
,如 .
.
(I)写出 的值;
的值;
(II) 若 求
求 的值;(只需写出结论)
的值;(只需写出结论)
(III)设 ,
, (
( ), 记数列
), 记数列 的前
的前 项和为
项和为 ,求
,求 ;并求正整数
;并求正整数 ,使得对任意
,使得对任意 ,均有
,均有 .
.
| 2 | 4 | 8 | 14 | … |
| 6 | 10 | 16 | 24 | … |
| 12 | 18 | 26 | 36 | … |
| 20 | 28 | 38 | 50 | … |
| … | … | … | … | … |
 满足
满足 ,若
,若 的最大值为13,则实数
的最大值为13,则实数 的值为( )
的值为( ) C.
C.  D. 5
D. 5 的公差是2,若
的公差是2,若 成等比数列,则
成等比数列,则  等于
等于 B.
B.  C.
C.  D.
D. 
 =(2,4),
=(2,4), =(1,3),则
=(1,3),则 ·
· =________.
=________. ,(a+b)·(a+3b)=33,则a与b的 夹角为________.
,(a+b)·(a+3b)=33,则a与b的 夹角为________. os A,cos B),向量p=
os A,cos B),向量p=
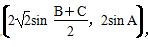 ,若m∥n,p2=9,求证:△ABC为等边三角形.
,若m∥n,p2=9,求证:△ABC为等边三角形. α=-
α=- ,α是第三象限的角,则sin(α+
,α是第三象限的角,则sin(α+ )=________.
)=________.