Question

如图，在棱长为1的正方体ABCD—A₁B₁C₁D₁中，E、F分别是D₁D、BD的中点，G在棱CD上，且CG=，应用空间向量的运算办法解决下列问题：

（1）求证：EF⊥B₁C；

（2）求EF与C₁G所成角的余弦；

（3）若A为C₁G的中点，求FH的长.

Answer 1

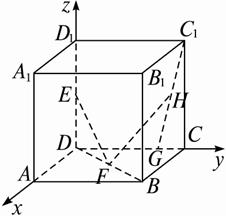
思路分析：利用空间向量的基础知识，证明异面直线垂直，求异面直线所成的角及线段的长度.

解：如图，建立空间直角坐标系O—xyz,

D为坐标原点O，由已知，有E（0，0，），F（，，0），C（0，1，0），C₁（0，1，1），B₁（1，1，1），G（0，，0）.

（1）∵=（，，0）-（0，0，）=（，，），

=（0，1，0）-（1，1，1）=（-1，0，-1），

∴=×(-1)+×0+()×(-1)=0.

∴.

∴EF⊥B₁C.

(2)∵=(0,,0)-(0,1,1)=(0,,-1),

∴||=.

    由（1），得||=.

    且=.

    所以cos＜＞==.

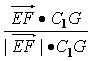（3）因为H是C₁G的中点，所以H（0，）.

    又F（2，0），

    故|FH|=||=.