题目内容
已知关于x函数f(x)=(1-a)x2+(a+2)x-4,a为实数,求:
(1)函数f(x)在[-2,1]只存在一个零点,求a的取值范围;
(2)函数f(x)的所有零点都大于0,求a的取值范围.
解:(1)∵函数在[-2,1]只存在一个零点,∴f(-2)×f(1)≤0.…(2分)
(等号不同时取),即:-1(-6a-4)≤0,解得: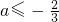 ,即a的取值范围为(-∞,-
,即a的取值范围为(-∞,- ]. …(5分)
]. …(5分)
(2)①当1-a=0时,即a=1,则3x-4=0,解得: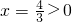 (符合题意).…(8分)
(符合题意).…(8分)
②当1-a≠0时,即a≠1,则满足: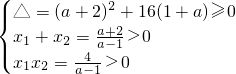 ,…(11分)
,…(11分)
推出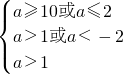 ,可得1<a≤2,或a≥10.…(13分)
,可得1<a≤2,或a≥10.…(13分)
综合以上情况,所求的a的取值范围为[1,2]∪[10,+∞). …(14分)
分析:(1)由函数在[-2,1]只存在一个零点,可得f(-2)×f(1)≤0 (等号不同时取),即:-1(-6a-4)≤0,由此求得a的取值范围.
(2)①当1-a=0时,即a=1,则3x-4=0,解得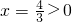 符合题意. ②当1-a≠0时,即a≠1,则由
符合题意. ②当1-a≠0时,即a≠1,则由 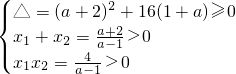 ,再求得a的取值范围.
,再求得a的取值范围.
最后将求得的两个a的取值范围取并集,即得所求.
点评:本题主要考查函数的零点的定义,函数的零点与方程的根的关系,体现了转化的数学思想,属于基础题.
(等号不同时取),即:-1(-6a-4)≤0,解得:
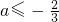 ,即a的取值范围为(-∞,-
,即a的取值范围为(-∞,- ]. …(5分)
]. …(5分)(2)①当1-a=0时,即a=1,则3x-4=0,解得:
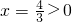 (符合题意).…(8分)
(符合题意).…(8分)②当1-a≠0时,即a≠1,则满足:
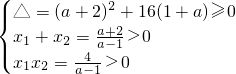 ,…(11分)
,…(11分)推出
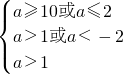 ,可得1<a≤2,或a≥10.…(13分)
,可得1<a≤2,或a≥10.…(13分)综合以上情况,所求的a的取值范围为[1,2]∪[10,+∞). …(14分)
分析:(1)由函数在[-2,1]只存在一个零点,可得f(-2)×f(1)≤0 (等号不同时取),即:-1(-6a-4)≤0,由此求得a的取值范围.
(2)①当1-a=0时,即a=1,则3x-4=0,解得
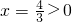 符合题意. ②当1-a≠0时,即a≠1,则由
符合题意. ②当1-a≠0时,即a≠1,则由 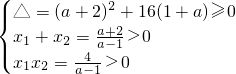 ,再求得a的取值范围.
,再求得a的取值范围.最后将求得的两个a的取值范围取并集,即得所求.
点评:本题主要考查函数的零点的定义,函数的零点与方程的根的关系,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
 已知关于x的二次函数f(x)=x2+ax-b(a,b∈R).
已知关于x的二次函数f(x)=x2+ax-b(a,b∈R).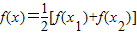 有两个不相等的实数根且必有一个根属于(x1,x2);
有两个不相等的实数根且必有一个根属于(x1,x2);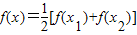 在(x1,x2)的根为m,且
在(x1,x2)的根为m,且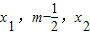 成等差数列,设函数f (x)的图象的对称轴方程为x=x,求证:x<m2.
成等差数列,设函数f (x)的图象的对称轴方程为x=x,求证:x<m2.