题目内容
甲、乙、丙、丁四名射击选手在选拔赛中所得的平均环数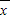
及其方差s2如下表所尔，则选送决赛的最住人选是 ．| 甲 | 乙 | 丙 | 丁 | |
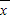 | 7 | 8 | 8 | 7 |
| s2 | 6.3 | 6.3 | 7 | 8.7 |
【答案】分析：甲，乙，丙，丁四个人中乙和丙的平均数最大且相等，甲，乙，丙，丁四个人中甲，乙的方差最小，说明乙的成绩最稳定，得到乙是最佳人选．
解答：解：∵甲，乙，丙，丁四个人中乙和丙的平均数最大且相等，
甲，乙，丙，丁四个人中乙的方差最小，
说明乙的成绩最稳定，
∴综合平均数和方差两个方面说明乙成绩即高又稳定，
∴乙是最佳人选，
故答案为：乙．
点评：本题考查随机抽样和一般估计总体的实际应用，考查对于平均数和方差的实际应用，对于几组数据，方差越小数据越稳定，这是经常考查的一种题目类型．
解答：解：∵甲，乙，丙，丁四个人中乙和丙的平均数最大且相等，
甲，乙，丙，丁四个人中乙的方差最小，
说明乙的成绩最稳定，
∴综合平均数和方差两个方面说明乙成绩即高又稳定，
∴乙是最佳人选，
故答案为：乙．
点评：本题考查随机抽样和一般估计总体的实际应用，考查对于平均数和方差的实际应用，对于几组数据，方差越小数据越稳定，这是经常考查的一种题目类型．
练习册系列答案
相关题目