题目内容
在△ABC中,已知∠ABC=45°,AB=
,D是BC边上的一点,AD=5,DC=3,求AC的长.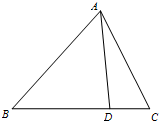
5
| ||
| 2 |

分析:在△ABD中,由正弦定理得,可得sin∠ADB=
=
,所以∠ADB=
或
,然后分∠ADB=
与∠ADB=
两种情况加以讨论,分别在△ADC中用余弦定理可得AC2的值,从而得到AC长为7或
.
| ABsinB |
| AD |
| ||
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| 19 |
解答:解:在△ABD中,由正弦定理得,
=
∴sin∠ADB=
=
=
又∵∠ADB∈(0,π),∴∠ADB=
或
,
①若∠ADB=
,则∠ADC=
,
在△ADC中,由余弦定理得AC2=AD2+DC2-2AD•DCcos∠ADC=49
∴AC=7,
②若∠ADB=
,则∠ADC=
,
在△ADC中,由余弦定理得AC2=AD2+DC2-2AD•DCcos∠ADC=19,
∴AC=
综上所述,AC长为7或
| AD |
| sin∠B |
| AB |
| sin∠ADB |
∴sin∠ADB=
| ABsinB |
| AD |
| ||||||
| 5 |
| ||
| 2 |
又∵∠ADB∈(0,π),∴∠ADB=
| π |
| 3 |
| 2π |
| 3 |
①若∠ADB=
| π |
| 3 |
| 2π |
| 3 |
在△ADC中,由余弦定理得AC2=AD2+DC2-2AD•DCcos∠ADC=49
∴AC=7,
②若∠ADB=
| 2π |
| 3 |
| π |
| 3 |
在△ADC中,由余弦定理得AC2=AD2+DC2-2AD•DCcos∠ADC=19,
∴AC=
| 19 |
综上所述,AC长为7或
| 19 |
点评:本题在△ABC中,给出∠B的度数和边AB长,BC边上的一点D到A、C两点的距离分别为5和3,求AC的长.着重考查了正弦定理和余弦定理及其应用,属于中档题.

练习册系列答案
相关题目