题目内容
有三个球,第一个球内切于正方体六个面,第二个球与这个正方体各条棱相切,第三个球过这个正方体的各个顶点,求这三个球的表面积之比.
设正方体的棱长为a.?
(1)正方体的内切球球心是正方体的中心,?
切点是六个面的中心,?
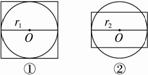
经过四个切点及球心作截面如图①,?
所以有2r1=a,![]() .
.
所以S1=4πr12=πa2.?
(2)球与正方体的各棱的切点在每条棱的中点,
过球心作正方体的对角面得截面,如图②,2r2=![]() ,
,![]() ,?
,?
所以S2=4πr22=2πa2.?
③
(3)正方体的各个顶点在球面上,?
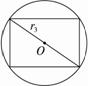
过球心作正方体的对角面得截面,?
如图③,所以有![]() ,
,![]() ,?
,?
所以S3=4πr32=3πa2.?
由上知:S1∶S2∶S3=1∶2∶3.
解析:
简单几何体和球

练习册系列答案
相关题目