题目内容
如图2-2-24,四边形ABCD是矩形,P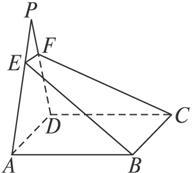
平面ABCD,过BC作平面BCFE交AP于E,交DP于F.求证:四边形BCFE是梯形.
图2-2-24
思路分析:证明BC∥EF,并且BC≠EF.
证明:因为四边形ABCD是矩形,所以BC∥AD,
因为BC
平面APD,BC平面APD,
所以BC∥平面APD.
因为平面BCFE∩平面APD=EF,
所以BC∥EF,所以AD∥EF.
又因为E、F是三角形APD边上的点,
所以EF≠AD,所以EF≠BC,
所以四边形BCFE是梯形.
练习册系列答案
口算小状元口算速算天天练系列答案
天天练口算系列答案
相关题目
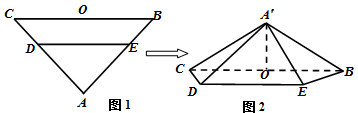
如图1，在等腰△ABC中，∠A=90°，BC=6，D，E分别是AC，AB上的点，CD=BE=
，O为BC的中点．将△ADE沿DE折起，得到如图2所示的四棱锥A′-BCDE．若A′O⊥平面BCDE，则A′D与平面A′BC所成角的正弦值等于（ ）
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
