题目内容
在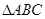 中,
中,
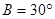 ,
,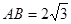 ,
,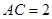 。则
。则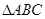 的面积是
.
的面积是
.
【答案】
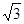 或
或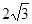
【解析】
试题分析:因为在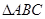 中,
中, 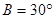 ,
,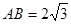 ,
,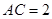 ,所以由正弦定理得:
,所以由正弦定理得: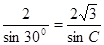 ,所以
,所以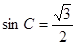 ,所以
,所以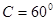 或
或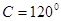 ,若
,若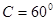 ,则
,则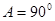 ,所以
,所以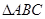 的面积
的面积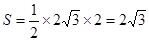 ;若
;若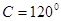 ,则
,则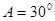 ,所以
,所以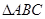 的面积
的面积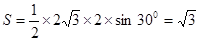 ,所以所求面积为
,所以所求面积为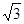 或
或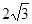 .
.
考点:1.正弦定理; 2.三角形的面积公式

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
在正方体ABCD-A1BC1D1中,点P在线段AD1上运动,则异面直线CP与BA1所成的角θ的取值范围是()?


A、0<θ<
| ||
B、0<θ≤
| ||
C、0≤θ≤
| ||
D、0<θ≤
|

 中,
中, ,
, ,
, ,则
,则 的长为 .
的长为 .