题目内容
 如图在△ABC中,D为BC边的中点.
如图在△ABC中,D为BC边的中点.| AM |
| AB |
| AN |
| AC |
| AP |
| AD |
(1)当m=1,n=
| 1 |
| 2 |
(2)当m,n∈(0,1)时,试用m,n表示x..
分析:(1)当m=1,n=
时,点P为△ABC的重心,由此能求出x的值.
,由M,P,N共线,知p+q=1.x
=pm
+qn
,又∵
=
(
+
),
(
+
)=pm
+qn
.由
与
不共线,能用用m,n表示x.
| 1 |
| 2 |
|
| AD |
| AB |
| AC |
| AD |
| 1 |
| 2 |
| AB |
| AC |
| x |
| 2 |
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
解答:解:(1)当m=1,n=
时,
点P为△ABC的重心,
∴x=
.
,
∵M,P,N共线
∴p+q=1
∴x
=pm
+qn
,又∵
=
(
+
)
∴
(
+
)=pm
+qn
∵
与
不共线
∴
⇒
+
=
即x=
| 1 |
| 2 |
点P为△ABC的重心,
∴x=
| 2 |
| 3 |
|
∵M,P,N共线
∴p+q=1
∴x
| AD |
| AB |
| AC |
| AD |
| 1 |
| 2 |
| AB |
| AC |
∴
| x |
| 2 |
| AB |
| AC |
| AB |
| AC |
∵
| AB |
| AC |
∴
|
| 1 |
| m |
| 1 |
| n |
| 2 |
| x |
| 2mn |
| m+n |
点评:本题考查向量在几何中的应用,解题时要认真审题,仔细解答,注意三角形的重心性质的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,△ABC中,D,E,F分别是边BC,AB,CA的中点,在以A、B、C、D、E、F为端点的有向线段中所表示的向量中,
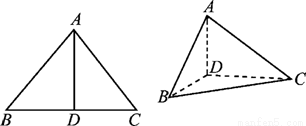
如图,△ABC中,D,E,F分别是边BC,AB,CA的中点,在以A、B、C、D、E、F为端点的有向线段中所表示的向量中, 13、13、如图在△ABC中,AD⊥BC,ED=2AE,过E作FG∥BC,且将△AFG沿FG折起,使∠EA'D=90°,则二面角A'-FG-B的大小为
13、13、如图在△ABC中,AD⊥BC,ED=2AE,过E作FG∥BC,且将△AFG沿FG折起,使∠EA'D=90°,则二面角A'-FG-B的大小为 (2012•珠海一模)(几何证明选讲选做题)
(2012•珠海一模)(几何证明选讲选做题)