题目内容
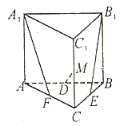
【题目】如图,在四棱锥![]() 中,已知
中,已知![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上一点.
上一点.
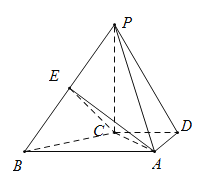
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,且二面角
的中点,且二面角![]() 的余弦值是
的余弦值是![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)先证明![]() 平面
平面![]() ,然后可得平面
,然后可得平面![]() 平面
平面![]() ;
;
(2)建立坐标系,根据二面角![]() 的余弦值是
的余弦值是![]() 可得
可得![]() 的长度,然后可求直线
的长度,然后可求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,得
,得![]() .
.
又![]() ,在
,在![]() 中,得
中,得![]() ,
,
设![]() 中点为
中点为![]() ,连接
,连接![]() ,则四边形
,则四边形![]() 为边长为1的正方形,所以
为边长为1的正方形,所以![]() ,且
,且![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)以![]() 为坐标原点,分别以射线
为坐标原点,分别以射线![]() 射线
射线![]() 为
为![]() 轴和
轴和![]() 轴的正方向,建立如图空间直角坐标系,
轴的正方向,建立如图空间直角坐标系,
则![]() ,
,![]() ,
,![]() .
.
又设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() .
.
由![]() 且
且![]() 知,
知,![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则![]() ,
,
即![]() ,取
,取![]() ,
,![]() ,则
,则![]() ,有
,有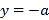 ,得
,得![]() ,从而
,从而![]() ,
,![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则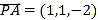
![]() .
.
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

 亮点激活精编提优100分大试卷系列答案
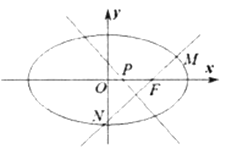
亮点激活精编提优100分大试卷系列答案【题目】已知椭圆![]() ,
,![]() 为椭圆
为椭圆![]() 的右焦点,
的右焦点, 为椭圆上一点,
为椭圆上一点,![]() 的离心率
的离心率![]()
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)斜率为![]() 的直线
的直线![]() 过点
过点![]() 交椭圆
交椭圆![]() 于
于![]() 两点,线段
两点,线段![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() ,试探究
,试探究![]() 是否为定值,如果是,请求出该定值;如果不是,请说明理由.
是否为定值,如果是,请求出该定值;如果不是,请说明理由.
【题目】某高校健康社团为调查本校大学生每周运动的时长,随机选取了80名学生,调查他们每周运动的总时长(单位:小时),按照![]()
![]()
![]()
![]()
![]()
![]() 共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
表1:男生
时长 |
|
|
|
|
|
|
人数 | 2 | 8 | 16 | 8 | 4 | 2 |
表2:女生
时长 |
|
|
|
|
|
|
人数 | 0 | 4 | 12 | 12 | 8 | 4 |
(1)从每周运动时长不小于20小时的男生中随机选取2人,求选到“运动达人”的概率;
(2)根据题目条件,完成下面![]() 列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
每周运动的时长小于15小时 | 每周运动的时长不小于15小时 | 总计 | |
男生 | |||
女生 | |||
总计 | |||
参考公式: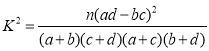 ,其中
,其中![]() .
.
参考数据:
| 0.40 | 0.25 | 0.10 | 0.010 |
| 0.708 | 1.323 | 2.706 | 6.635 |