题目内容
(本小题满分13分)已知函数 ,
, .
.
(Ⅰ)设 (其中
(其中 是
是 的导函数),求
的导函数),求 的最大值;
的最大值;
(Ⅱ)求证: 当 时,有
时,有 ;
;
(Ⅲ)设 ,当
,当 时,不等式
时,不等式 恒成立,求
恒成立,求 的最大值.
的最大值.
(Ⅰ)当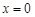 时,
时,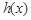 取得最大值
取得最大值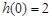 ;
;
(Ⅱ)当 时,
时,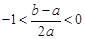 .由(1)知:当
.由(1)知:当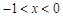 时,
时,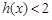 ,即
,即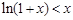 .
.
因此,有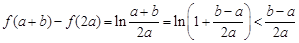 .
.
(Ⅲ)整数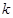 的最大值是
的最大值是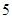 .
.
解析试题分析:(Ⅰ)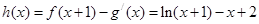 ,
,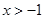 所以
所以  .
.
当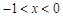 时,
时,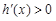 ;当
;当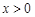 时,
时,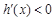 .
.
因此,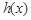 在
在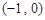 上单调递增,在
上单调递增,在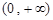 上单调递减.
上单调递减.
因此,当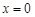 时,
时,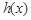 取得最大值
取得最大值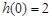 ; ………………3分
; ………………3分
(Ⅱ)当 时,
时,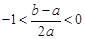 .由(1)知:当
.由(1)知:当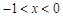 时,
时,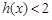 ,即
,即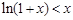 .
.
因此,有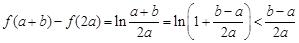 .………………7分
.………………7分
(Ⅲ)不等式 化为
化为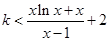 所以
所以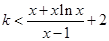 对任意
对任意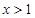 恒成立.令
恒成立.令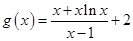 ,则
,则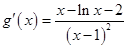 ,
,
令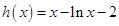
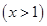 ,则
,则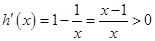 ,所以函数
,所以函数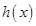 在
在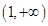 上单调递增.
上单调递增.
因为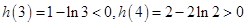 ,
,
所以方程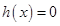 在
在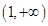 上存在唯一实根
上存在唯一实根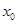 ,且满足
,且满足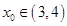 .
.
当 ,即
,即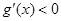 ,当
,当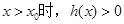 ,即
,即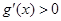 ,
,
所以函数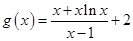 在
在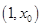 上单调递减,在
上单调递减,在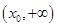 上单调递增.
上单调递增.
所以 .
.
所以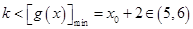 .故整数
.故整数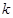 的最大值是
的最大值是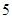 . ……………13分
. ……………13分
考点:本题主要考查了导数的运算、导数在函数单调性及不等式中的应用。
点评:较难题,利用导数求函数单调区间的方法,解题时注意函数的定义域,避免出错。

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 .
. 在
在 和
和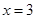 处的切线互相平行,求
处的切线互相平行,求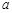 的值;
的值; 的单调区间;
的单调区间; ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求
,求 ,设其定义域域是
,设其定义域域是 .
.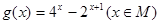 的值域.
的值域. 的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为
的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为 ,容积为
,容积为 .
.
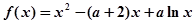 ,其中常数
,其中常数 。
。 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;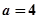 时,是否存在实数
时,是否存在实数 ,使得直线
,使得直线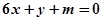 恰为曲线
恰为曲线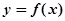 的切线?若存在,求出
的切线?若存在,求出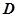 上的函数
上的函数 的图象在点
的图象在点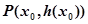 处的切线方程为
处的切线方程为 ,当
,当 时,若
时,若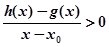 在
在 为函数
为函数 是定义在
是定义在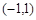 上的奇函数,当
上的奇函数,当 时
时 且
且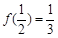 。
。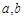 的值;
的值;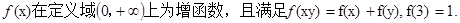
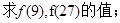

 .
. 的值域为
的值域为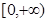 ,求a的值;
,求a的值; 上是增函数,求实数
上是增函数,求实数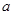 的取值范围.
的取值范围. 。
。 的定义域;
的定义域;