题目内容
设![]() ,其中
,其中![]() ,且
,且![]() (
(![]() 为自然对数的底数)
为自然对数的底数)
(I)求![]() 与
与![]() 的关系;
的关系;
(II)若![]() 在其定义域内为单调函数,求
在其定义域内为单调函数,求![]() 的取值范围;
的取值范围;
(III)证明:
① ![]() ;
;
② ![]() .
.
解:(I)由题意知![]() ,
,
又![]() ,
,
∴![]() ,
,
∴ ![]() ,即
,即![]() ,
,
而![]() ,
,
∴ ![]() .
.
(II)由(I)知![]() ,
,
![]() ,
,
令![]() ,要使
,要使![]() 在其定义域
在其定义域![]() 内为单调函数,只需
内为单调函数,只需![]() 在
在![]() 内满足:
内满足:![]() 或
或![]() 恒成立.
恒成立.
① 当![]() 时,
时,![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 内为单调递减,故
内为单调递减,故![]() 适合题意.
适合题意.
② 当![]() 时,
时,![]() ,其图象为开口向上的抛物线,对称轴为
,其图象为开口向上的抛物线,对称轴为![]()
![]() , ∴
, ∴![]() .
.
只需![]() ,即
,即![]() 时
时![]() ,
,![]() ,
,
∴![]() 在
在![]() 内为单调递增,
内为单调递增,
故![]() 适合题意.
适合题意.
③当![]() 时,
时,![]() ,其图象为开口向下的抛物线,对称轴为
,其图象为开口向下的抛物线,对称轴为![]()
![]() .
.
只需![]() ,即
,即![]() 时
时![]() 在
在![]() 恒成立.
恒成立.
故![]() 适合题意.
适合题意.
综上可得,![]() 或
或![]() .
.
(III)证明:①即证明 ![]() ,
,
设![]() ,
,![]() ,
,
∴ ![]() 时,
时,![]() ,∴
,∴ ![]() 为单调递增函数;
为单调递增函数;
![]() 时,
时,![]() ,∴
,∴ ![]() 为单调递减函数;
为单调递减函数;
![]() 为
为![]() 的极大值点.
的极大值点.
∴![]() , 即
, 即![]() ∴
∴![]()
② 由(I)知![]() ,又
,又![]() ,
,
设![]() ,则
,则![]() , ∴
, ∴![]() .
.
∵ ![]() , ∴
, ∴![]()
∴ ![]() ,
,
∴![]() ,
,

∴ 结论成立.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
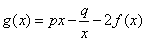 ,其中
,其中 ,且
,且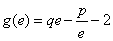 (
(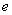 为自然对数的底)
为自然对数的底)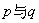 的关系;
的关系;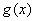 在其定义域内的单调函数,求
在其定义域内的单调函数,求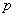 的取值范围;
的取值范围;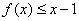
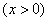
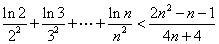 (
(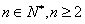 )。
)。