题目内容
已知直线l1经过点A(2,a),B(a-1,3),直线l2经过点C(1,2),D(-3,a+2).(1)若l1∥l2,求a的值;
(2)若l1⊥l2,求a的值.
【答案】分析:设直线l1、l2的斜率分别为k1、k2,因为直线l2 ;;的斜率 ;;k2 一定存在,且不等于0,
先检验k1不存在的情况,即a=3时,得到l1与l2既不平行,也不垂直,故a不等于3,两直线的斜率都存在.
(1)若l1∥l2,则 k1=k2 ;;,解出a值,并验证直线l1与l2不重合,
(2)若 l1⊥l2,则则斜率之积等于-1,即 k1k2=-1,解出a值.
解答:解:设直线l1、l2的斜率分别为k1、k2,若a=3,则k1不存在,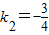 ,则l1与l2既不平行,也不垂直.
,则l1与l2既不平行,也不垂直.
因此a≠3,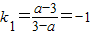 ,
,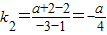 .
.
(1)∵l1∥l2,∴k1=k2
∴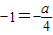 .
.
∴a=4,经检验,a=4 时,两直线平行
(2)∵l1⊥l2,∴k1k2=-1.
∴(-1)(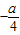 )=-1.
)=-1.
∴a=-4.
点评:本题考查两条直线平行与垂直的条件.两直线平行时,除了斜率相等外,
还要求它们在坐标轴上的截距不相等,(仅有斜率相等时,两直线有可能重合,故需检验).
先检验k1不存在的情况,即a=3时,得到l1与l2既不平行,也不垂直,故a不等于3,两直线的斜率都存在.
(1)若l1∥l2,则 k1=k2 ;;,解出a值,并验证直线l1与l2不重合,
(2)若 l1⊥l2,则则斜率之积等于-1,即 k1k2=-1,解出a值.
解答:解:设直线l1、l2的斜率分别为k1、k2,若a=3,则k1不存在,
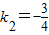 ,则l1与l2既不平行,也不垂直.
,则l1与l2既不平行,也不垂直.因此a≠3,
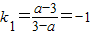 ,
,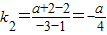 .
.(1)∵l1∥l2,∴k1=k2
∴
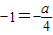 .
.∴a=4,经检验,a=4 时,两直线平行
(2)∵l1⊥l2,∴k1k2=-1.
∴(-1)(
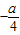 )=-1.
)=-1.∴a=-4.
点评:本题考查两条直线平行与垂直的条件.两直线平行时,除了斜率相等外,
还要求它们在坐标轴上的截距不相等,(仅有斜率相等时,两直线有可能重合,故需检验).

练习册系列答案
相关题目