题目内容
设函数f(x)=![]() (x-3a)(a>0,且a≠1),当点P(x,y)是函数y=f(x)图象上的点时,点Q(x-2a,-y)是函数y=g(x)图象上的点.
(x-3a)(a>0,且a≠1),当点P(x,y)是函数y=f(x)图象上的点时,点Q(x-2a,-y)是函数y=g(x)图象上的点.
(Ⅰ)写出函数y=g(x)的解析式;
(Ⅱ)若当x∈[a+2,a+3]时,恒有|f(x)-g(x)|≤1,试确定a的取值范围.
答案:
解析:
解析:
|
(1)设点Q的坐标为 即x= ∵点P(x,y)在函数y= ∴ ∴g(x)= (2)由题意,x-3a=(a+2)-3a=-2a+2>0; 又a>0,且a≠1, ∴0<a<1. ∵|f(x)-g(x)|=| |f(x)-g(x)|≤1, ∴-1≤ ∵0<a<1, ∴a+2>2a,r(x)= ∴函数,μ(x)= 从而, 于是所求问题转化求不等式组 由 由 ∴所求a的取值范围是0<a≤ |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则
,则 =x-2a,
=x-2a, =-y,
=-y, +2a,y=-y.
+2a,y=-y. (x-3a)的图象上,
(x-3a)的图象上,
 .
. =
= >0.
>0. (x-3a)-
(x-3a)- |=|
|=| )|,
)|, ≤1.
≤1. 在[a+2,a+3]上为增函数,
在[a+2,a+3]上为增函数, =μ(a+2)=
=μ(a+2)= =μ(a+3)=
=μ(a+3)=

 ,
,
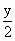 )是函数y=g(x)图象上的点.
)是函数y=g(x)图象上的点. ,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为________.
,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为________.