题目内容
在△ABC中,已知tanB=解:设AB、BC、CA的长分别为c、a、b.由tanB=![]() ,得B=60°,∴sinB=
,得B=60°,∴sinB=![]() ,cosB=
,cosB=![]() .又sinC=
.又sinC=![]() =
=![]() ,应用正弦定理得c=
,应用正弦定理得c=![]() =
=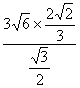 =8.∴sinA=sin(B+C)=sinB·cosC+cosB·sinC=
=8.∴sinA=sin(B+C)=sinB·cosC+cosB·sinC=![]() ×
×![]() +
+![]() ×
×![]() =
=![]() +
+![]() .?故所求面积S△ABC=
.?故所求面积S△ABC=![]() bcsinA=6
bcsinA=6![]() +8
+8![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
在△ABC中,已知tanB=解:设AB、BC、CA的长分别为c、a、b.由tanB=![]() ,得B=60°,∴sinB=
,得B=60°,∴sinB=![]() ,cosB=
,cosB=![]() .又sinC=
.又sinC=![]() =
=![]() ,应用正弦定理得c=
,应用正弦定理得c=![]() =
=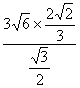 =8.∴sinA=sin(B+C)=sinB·cosC+cosB·sinC=
=8.∴sinA=sin(B+C)=sinB·cosC+cosB·sinC=![]() ×
×![]() +
+![]() ×
×![]() =
=![]() +
+![]() .?故所求面积S△ABC=
.?故所求面积S△ABC=![]() bcsinA=6
bcsinA=6![]() +8
+8![]() .
.

 名校课堂系列答案
名校课堂系列答案