题目内容
如图,三棱柱ABC—A1B1C1的侧棱AA1⊥底面ABC,∠ACB = 90°,E是棱CC1上动点,F是AB中点,AC = 1,BC = 2,AA1 = 4.
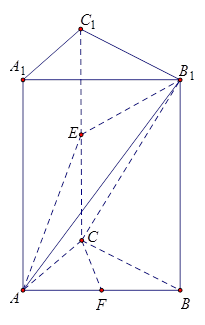
(Ⅰ)当E是棱CC1中点时,求证:CF∥平面AEB1;
(Ⅱ)在棱CC1上是否存在点E,使得二面角A—EB1—B的余弦值是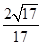 ,若存在,求CE的长,若不存在,请说明理由.
,若存在,求CE的长,若不存在,请说明理由.

(Ⅰ)当E是棱CC1中点时,求证:CF∥平面AEB1;
(Ⅱ)在棱CC1上是否存在点E,使得二面角A—EB1—B的余弦值是
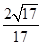 ,若存在,求CE的长,若不存在,请说明理由.
,若存在,求CE的长,若不存在,请说明理由.(Ⅰ)详见试题解析;(Ⅱ)在棱 上存在点
上存在点 使得二面角A—EB1—B的余弦值是
使得二面角A—EB1—B的余弦值是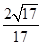 ,且
,且
 上存在点
上存在点 使得二面角A—EB1—B的余弦值是
使得二面角A—EB1—B的余弦值是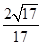 ,且
,且
试题分析:(Ⅰ)根据直线平行平面的判定定理,需要在平面AEB1内找一条与CF平行的直线.根据题设,可取
 的中点
的中点 ,通过证明四边形
,通过证明四边形 是平行四边形来证明
是平行四边形来证明 ,从而使问题得证;(Ⅱ)由于
,从而使问题得证;(Ⅱ)由于 两两垂直,故可以
两两垂直,故可以 为坐标原点,射线
为坐标原点,射线 为
为 轴的正半轴建立空间坐标系,利用空间向量求解.
轴的正半轴建立空间坐标系,利用空间向量求解.试题解析:(Ⅰ)证明:取
 的中点
的中点 ,联结
,联结
∵
 分别是棱
分别是棱 、
、 的中点,
的中点,∴

又∵

∴四边形
 是平行四边形,
是平行四边形,∴

∵
 平面
平面 ,
, 平面
平面
∴
 平面
平面
(Ⅱ)解:由于
 两两垂直,故可以
两两垂直,故可以 为坐标原点,射线
为坐标原点,射线 为
为 轴的正半轴建立空间坐标系如图所示
轴的正半轴建立空间坐标系如图所示则

设
 ,平面
,平面 的法向量
的法向量 ,
,则

由

得
 ,取
,取 得:
得:
∵
 平面
平面
∴
 是平面
是平面 的法向量,则平面
的法向量,则平面 的法向量
的法向量
∵二面角
 的平面角的余弦值为
的平面角的余弦值为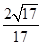
∴

解之得

∴在棱
 上存在点
上存在点 使得二面角A—EB1—B的余弦值是
使得二面角A—EB1—B的余弦值是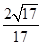 ,且
,且 .
.
练习册系列答案
相关题目
 中,
中,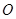 、
、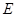 分别是
分别是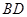 、
、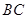 的中点,
的中点,
 平面
平面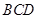 ;
;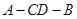 的正切值;
的正切值;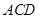 的距离.
的距离.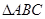 中,
中,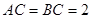 ,
,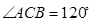 ,
,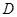 为
为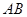 的中点,
的中点,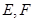 分别在线段
分别在线段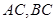 上的动点,且
上的动点,且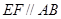 ,
,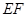 交
交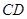 于
于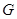 ,把
,把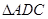 沿
沿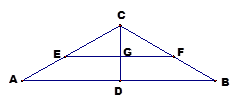
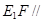 平面
平面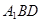 ;
;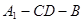 为直二面角时,是否存在点
为直二面角时,是否存在点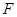 ,使得直线
,使得直线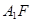 与平面
与平面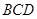 所成的角为
所成的角为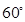 ,若存在求
,若存在求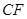 的长,若不存在说明理由。
的长,若不存在说明理由。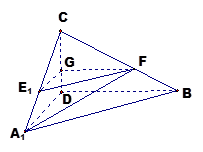
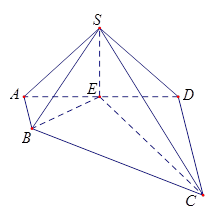
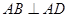 ,
,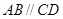 ,
,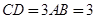 ,平面
,平面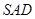 ⊥平面
⊥平面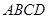 ,
,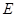 是线段
是线段 上一点,
上一点,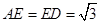 ,
,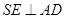 .
.
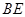 ⊥平面
⊥平面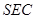 ;
;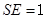 ,求直线
,求直线 与平面
与平面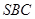 所成角的正弦值.
所成角的正弦值.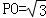 ,E、F分别是BC、AP的中点.
,E、F分别是BC、AP的中点.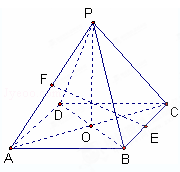
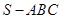 中,已知点
中,已知点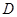 、
、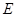 、
、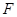 分别为棱
分别为棱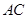 、
、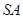 、
、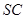 的中点.
的中点.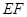 ∥平面
∥平面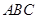 ;
;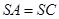 ,
,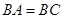 ,求证:平面
,求证:平面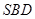 ⊥平面
⊥平面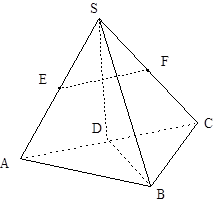
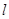 为直线,
为直线,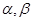 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )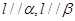 ,则
,则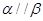
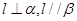 ,则
,则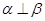
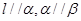 ,则
,则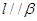
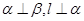 ,则
,则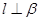
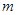 ,
,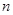 和一个平面
和一个平面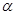 ,下列命题中的真命题是( )
,下列命题中的真命题是( )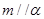 ,
, ,则
,则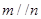
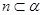 ,则
,则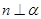 ,则
,则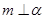 ,
,