题目内容
设函数f(x)=-x3-2mx2-m2x+1-m(m>-2)的图象在x=2处的切线与直线x-5y-12=0垂直.
(Ⅰ)求函数f(x)的极值与零点;
(Ⅱ)设g(x)=
+lnx,若对任意x1∈[0,1],存在x2∈(0,1],使f(x1)>g(x2)成立,求实数k的取值范围.
(Ⅰ)求函数f(x)的极值与零点;
(Ⅱ)设g(x)=
| 1-x | kx |
分析:(I)求出函数的导函数,结合函数f(x)的图象在x=2处的切线与直线x-5y-12=0垂直,可求出m值,进而得到函数f(x)及其导函数的解析式,列表分析函数的单调性,可得函数f(x)的极值与零点;
(Ⅱ)若对任意x1∈[0,1],存在x2∈(0,1],使f(x1)>g(x2)成立,可得函数f(x)在区间[0,1]上的最小值大于g(x)在区间(0,1]上的最小值,分类讨论后,综合讨论结果可得实数k的取值范围.
(Ⅱ)若对任意x1∈[0,1],存在x2∈(0,1],使f(x1)>g(x2)成立,可得函数f(x)在区间[0,1]上的最小值大于g(x)在区间(0,1]上的最小值,分类讨论后,综合讨论结果可得实数k的取值范围.
解答:解:(Ⅰ)∵f'(x)=-3x2-4mx-m2,所以f'(2)=-12-8m-m2=-5,
解得m=-1或m=-7
∵m>-2,∴m=-1
∴f'(x)=-3x2+4x-1,
f'(x)=-3x2+4x-1=0,解得x1=1,x2=
,
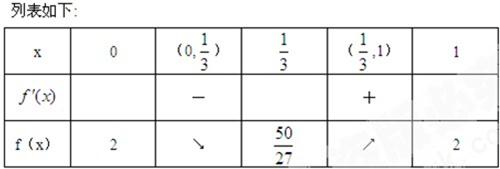
∴函数f(x)的极小值为f(
)=
.函数f(x)的极大值为f(1)=2.
∵f(x)=-x3+2x2-x+2=-(x-2)(x2+1)
∴函数f(x)的零点是2
(II)由(I)知,当x∈[0,1]时,f(x)min=
.
故“对任意x1∈[0,1],存在x2∈(0,1],使f(x1)>g(x2)成立”,等价于“函数f(x)在区间[0,1]上的最小值大于g(x)在区间(0,1]上的最小值”
即当x∈[0,1]时,g(x)min<
.
∵g(x)=
+lnx,
∴g′(x)=-
+
=
①当k<0时,因为x∈[0,1],故g(x)=
+lnx≤0<
,符号题意;
②当0<k≤1时,
≥1,故x∈[0,1]时,g′(x)≤0,g(x)单调递减
∴g(x)min=g(1)=0<
,符号题意;
③当k>1时,0<
<1,
则当x∈(0,
)时,g′(x)<0,g(x)单调递减
当x∈(
,1)时,g′(x)>0,g(x)单调递增
∴x∈[0,1]时,g(x)min=g(
)=1-
+ln
令h(x)=lnx-x-
(0<x<1)
则h′(x)=
-1>0
即h(x)在(0,1)上单调递增
∴x∈(0,1)时,h(x)<h(1)=-
<0,即lnx-x<
∴g(x)min=g(
)=1-
+ln
<1+
=
,符号题意;
综上所述,对于任意x1∈[0,1],存在x2∈(0,1],使f(x1)>g(x2)成立
则实数k的取值范围是(-∞,0)∪(0,+∞)
解得m=-1或m=-7
∵m>-2,∴m=-1
∴f'(x)=-3x2+4x-1,
f'(x)=-3x2+4x-1=0,解得x1=1,x2=
| 1 |
| 3 |

∴函数f(x)的极小值为f(
| 1 |
| 3 |
| 50 |
| 27 |
∵f(x)=-x3+2x2-x+2=-(x-2)(x2+1)
∴函数f(x)的零点是2
(II)由(I)知,当x∈[0,1]时,f(x)min=
| 50 |
| 27 |
故“对任意x1∈[0,1],存在x2∈(0,1],使f(x1)>g(x2)成立”,等价于“函数f(x)在区间[0,1]上的最小值大于g(x)在区间(0,1]上的最小值”
即当x∈[0,1]时,g(x)min<
| 50 |
| 27 |
∵g(x)=
| 1-x |
| kx |
∴g′(x)=-
| 1 |
| kx2 |
| 1 |
| x |
x-
| ||
| x2 |
①当k<0时,因为x∈[0,1],故g(x)=
| 1-x |
| kx |
| 50 |
| 27 |
②当0<k≤1时,
| 1 |
| k |
∴g(x)min=g(1)=0<
| 50 |
| 27 |
③当k>1时,0<
| 1 |
| k |
则当x∈(0,
| 1 |
| k |
当x∈(
| 1 |
| k |
∴x∈[0,1]时,g(x)min=g(
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
令h(x)=lnx-x-
| 23 |
| 27 |
则h′(x)=
| 1 |
| x |
即h(x)在(0,1)上单调递增
∴x∈(0,1)时,h(x)<h(1)=-
| 50 |
| 27 |
| 23 |
| 27 |
∴g(x)min=g(
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
| 23 |
| 27 |
| 50 |
| 27 |
综上所述,对于任意x1∈[0,1],存在x2∈(0,1],使f(x1)>g(x2)成立
则实数k的取值范围是(-∞,0)∪(0,+∞)
点评:本题考查的知识点是函数在某点取得极值的条件,导数在最大值,最小值问题中的应用,熟练掌握导数在求函数单调区间及极值时的方法和步骤是解答的关键.

练习册系列答案
相关题目
设函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A),有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t低调函数.如果定义域为[0,+∞)的函数f(x)=-|x-m2|+m2,且 f(x)为[0,+∞)上的10低调函数,那么实数m的取值范围是( )
| A、[-5,5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|