题目内容
已知双曲线与椭圆
+
=1共焦点，它们的离心率之和为
（1）求双曲线的焦点坐标；
（2）求双曲线的方程，写出渐近线方程和顶点坐标．
| x2 |
| 25 |
| y2 |
| 9 |
| 14 |
| 5 |
（1）求双曲线的焦点坐标；
（2）求双曲线的方程，写出渐近线方程和顶点坐标．
分析：利用椭圆与双曲线的标准方程和性质即可得出．
解答：解：（1）∵c=
=4，∴椭圆
+
=1的焦点为（±4，0），即双曲线的焦点为（±4，0）．
（2）设要求的双曲线方程为
-
=1，又椭圆与双曲线的离心率之和为
，
∴
+
=
，解得a=2，∴b=
=2
，
∴双曲线的方程为
-
=1，
渐近线方程为y=±
x，
顶点坐标为（±2，0）．
| 25-9 |
| x2 |
| 25 |
| y2 |
| 9 |
（2）设要求的双曲线方程为
| x2 |
| a2 |
| y2 |
| b2 |
| 14 |
| 5 |
∴
| 4 |
| 5 |
| 4 |
| a |
| 14 |
| 5 |
| 42-22 |
| 3 |
∴双曲线的方程为
| x2 |
| 4 |
| y2 |
| 12 |
渐近线方程为y=±
| 3 |
顶点坐标为（±2，0）．
点评：熟练掌握椭圆与双曲线的标准方程和性质是解题的关键．
练习册系列答案
相关题目
＝0，求双曲线的方程．
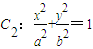有公共焦点F1F2，点
是它们的一个公共点．