题目内容
已知锐角α、β满足sinα=(1)求cos(α-β);
(2)求α+β.
解析:∵α、β为锐角且sinα=![]() ,cosβ=
,cosβ=![]() ,
,
∴cosα=![]() =
=![]() ,
,
sinβ=![]() =
=![]() .
.
(1)cos(α-β)=cosαcosβ+sinαsinβ
=![]() ·
·![]() +
+![]() ·
·![]() =
=![]() .
.
(2)cos(α+β)=cosαcosβ-sinαsinβ
=![]() ·
·![]() -
-![]() ·
·![]() =
=![]() .
.
∵0<α<![]() ,0<β<
,0<β<![]() ,
,
∴0<α+β<π.
又cos(α+β)>0,∴0<α+β<![]() .
.
∴α+β=![]() .
.
点评:要求cos(α+β)和cos(α-β)的值,需要知道sinα、cosα、sinβ、cosβ四个值,当已知α、β的一个三角函数值时,首先要根据同角三角函数基本关系式及角α、β的范围求出这四个值,然后用和差角余弦公式.求角应先分析角的范围,再求某一函数值,由角的范围和函数值才能给出角的大小.此题求α+β的正弦就不易给出α+β的值.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
 已知椭圆C:
已知椭圆C: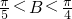 时,求△ABC的三边长及角B(用反三角函数值表示);
时,求△ABC的三边长及角B(用反三角函数值表示);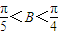 时,求△ABC的三边长及角B(用反三角函数值表示);
时,求△ABC的三边长及角B(用反三角函数值表示);