题目内容
在高三年级某班组织的欢庆元旦活动中,有一项游戏规则如下:参与者最多有5次抽题并答题的机会.如果累计答对2道题,立即结束游戏,并获得纪念品;如果5次机会用完仍未累计答对2道题,也结束游戏,并不能获得纪念品.已知某参与者答对每道题答对的概率都是 ,且每道题答对与否互不影响.
,且每道题答对与否互不影响.
(1)求该参与者获得纪念品的概率;
(2)记该参与者游戏时答题的个数为ξ,求ξ的分布列及期望.
解:(1)设“参与者获得纪念品”为事件A,则
P(A)=1-P =1-[(
=1-[( )5+
)5+ (
( )4(
)4( )]=
)]= .(4分)
.(4分)
故该参与者获得纪念品的概率为 .(5分)
.(5分)
(2)ξ的可能取值为2,3,4,5,
P(ξ=2)=( )2=
)2= ;P(ξ=3)=
;P(ξ=3)=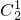
 •
• •
• =
= ;
;
P(ξ=4)=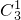
 (
( )2
)2 =
= ;P(ξ=5)=
;P(ξ=5)= (
( )(
)( )3+
)3+ (
( )4=
)4= .(8分)
.(8分)
故ξ的分布列为
Eξ=2× +3×
+3× +4×
+4× +5×
+5× =
= .(12分)
.(12分)
分析:(1)设“参与者获得纪念品”为事件A,求出其对立事件的概率,即可得到结论;
(2)ξ的可能取值为2,3,4,5,求出相应的概率,即可得到ξ的分布列及期望.
点评:本题考查概率的求法,考查离散型随机变量的分布列与期望,理解变量的取值及含义是关键.
P(A)=1-P
 =1-[(
=1-[( )5+
)5+ (
( )4(
)4( )]=
)]= .(4分)
.(4分)故该参与者获得纪念品的概率为
 .(5分)
.(5分)(2)ξ的可能取值为2,3,4,5,
P(ξ=2)=(
 )2=
)2= ;P(ξ=3)=
;P(ξ=3)=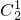
 •
• •
• =
= ;
;P(ξ=4)=
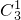
 (
( )2
)2 =
= ;P(ξ=5)=
;P(ξ=5)= (
( )(
)( )3+
)3+ (
( )4=
)4= .(8分)
.(8分)故ξ的分布列为
| ξ | 2 | 3 | 4 | 5 |
| P |  |  |  |  |
 +3×
+3× +4×
+4× +5×
+5× =
= .(12分)
.(12分)分析:(1)设“参与者获得纪念品”为事件A,求出其对立事件的概率,即可得到结论;
(2)ξ的可能取值为2,3,4,5,求出相应的概率,即可得到ξ的分布列及期望.
点评:本题考查概率的求法,考查离散型随机变量的分布列与期望,理解变量的取值及含义是关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 ,求
,求 ,且每道题答对与否互不影响.
,且每道题答对与否互不影响.