题目内容
已知点S是正三角形ABC所在平面外的一点,且SA=SB=SC,SG为△SAB上的高,D、E、F分别是AC、BC、SC的中点,试判断SG与平面DEF的位置关系,并给予证明.
探究1:如图,观察图形,即可判定SG∥平面DEF,要证明结论成立,只需证明SG与平面DEF内的一条直线平行.
证法1:连结CG交DE于点H,
∵DE是△ABC的中位线,∴DE∥AB.
在△ACG中,D是AC的中点,且DH∥AG,
∴H为CG的中点.
∵FH是△SCG的中位线,∴FH∥SG.
又SG![]() 平面DEF,FH
平面DEF,FH![]() 平面DEF,
平面DEF,
∴SG∥平面DEF.
探究2:要证明SG∥平面DEF,只需证明平面SAB∥平面DEF,要证明平面DEF∥平面SAB,只需证明SA∥DF,SB∥EF而SA∥DF,SB∥EF可由题设直接推出.
证法2:∵EF为△SBC的中位线,∴EF∥SB.
∵EF![]() 平面SAB,SB
平面SAB,SB![]() 平面SAB,
平面SAB,
∴EF∥平面SAB.
同理:DF∥平面SAB,EF∩DF=F,
∴平面SAB∥平面DEF,又∵SG![]() 平面SAB,
平面SAB,
∴SG∥平面DEF.

练习册系列答案
相关题目
 上,以M为圆心的圆与x轴相切于椭圆的右焦点,若圆M与y轴相交于A,B两点,且△ABM是边长为
上,以M为圆心的圆与x轴相切于椭圆的右焦点,若圆M与y轴相交于A,B两点,且△ABM是边长为 的正三角形,
的正三角形, ,求直线l的斜率;
,求直线l的斜率;  左半部分交于H,K两点,又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R,S两点,试判断满足
左半部分交于H,K两点,又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R,S两点,试判断满足 的直线GK是否存在?请说明理由。
的直线GK是否存在?请说明理由。 =1(a>b>0)上,以M为圆心的圆与x轴相切于椭圆的右焦点,若圆M与y轴相交于A,B两点,且△ABM是边长为
=1(a>b>0)上,以M为圆心的圆与x轴相切于椭圆的右焦点,若圆M与y轴相交于A,B两点,且△ABM是边长为 的正三角形.
的正三角形.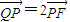 ,求直线l的斜率;
,求直线l的斜率; 左半部分交于H,K两点,又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R,S两点,试判断满足|GH|•|GK|=3|RF1|•|F1S|的直线GK是否存在?请说明理由.
左半部分交于H,K两点,又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R,S两点,试判断满足|GH|•|GK|=3|RF1|•|F1S|的直线GK是否存在?请说明理由.