题目内容
设Sn为数列{an}的前n项和,若 (n∈N*)是非零常数,则称该数列为“和等比数列”,
(n∈N*)是非零常数,则称该数列为“和等比数列”,
(1)若数列{ }是首项为2,公比为4的等比数列,试判断数列{bn}是否为“和等比数列”;
}是首项为2,公比为4的等比数列,试判断数列{bn}是否为“和等比数列”;
(2)若数列{cn}是首项为c1,公差为d(d≠0)的等差数列,且数列{cn}是“和等比数列”,试探究d与c1之间的等量关系.
 (n∈N*)是非零常数,则称该数列为“和等比数列”,
(n∈N*)是非零常数,则称该数列为“和等比数列”,(1)若数列{
 }是首项为2,公比为4的等比数列,试判断数列{bn}是否为“和等比数列”;
}是首项为2,公比为4的等比数列,试判断数列{bn}是否为“和等比数列”;(2)若数列{cn}是首项为c1,公差为d(d≠0)的等差数列,且数列{cn}是“和等比数列”,试探究d与c1之间的等量关系.
解:(1)因为数列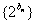 是首项为2,公比为4的等比数列,
是首项为2,公比为4的等比数列,
所以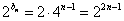 ,
,
因此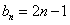 ;
;
设数列{bn}的前n项和为Tn,则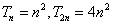 ,所以
,所以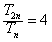 ,
,
因此数列{bn}为“和等比数列”.
(2)设数列{cn}的前n项和为Rn,且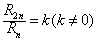 ,
,
因为数列{cn}是等差数列,所以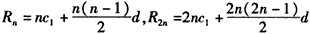 ,
,
所以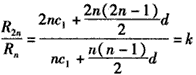 对于n∈N*都成立,
对于n∈N*都成立,
化简得,(k-4)dn+(k-2)(2c1-d)=0,
则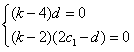 ,
,
因为d≠0,所以k=4,d=2c1,
因此d与c1之间的等量关系为d=2c1.
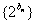 是首项为2,公比为4的等比数列,
是首项为2,公比为4的等比数列,所以
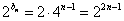 ,
,因此
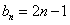 ;
;设数列{bn}的前n项和为Tn,则
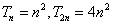 ,所以
,所以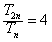 ,
,因此数列{bn}为“和等比数列”.
(2)设数列{cn}的前n项和为Rn,且
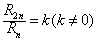 ,
,因为数列{cn}是等差数列,所以
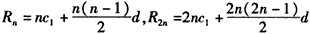 ,
,所以
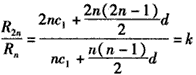 对于n∈N*都成立,
对于n∈N*都成立,化简得,(k-4)dn+(k-2)(2c1-d)=0,
则
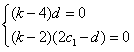 ,
,因为d≠0,所以k=4,d=2c1,
因此d与c1之间的等量关系为d=2c1.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目