题目内容
设函数 是奇函数,(a,b,c都是整数),且f(1)=2,f(2)<3,f(x)在[1,+∞)上单调递增.
是奇函数,(a,b,c都是整数),且f(1)=2,f(2)<3,f(x)在[1,+∞)上单调递增.(1)求a,b,c的值;
(2)当x<0时,f(x)的单调性如何?证明你的结论.
【答案】分析:(1)求三个未知数,需要三个条件,一是定义域要关于原点对称,二是f(1)=2,三是f(2)<3,f(x)在[1,+∞)上单调递增可解.
(2)用单调性定义来探讨,先在给定的区间上任取两个变量,且界定大小,再作差变形,在与0比较中出现讨论,再进一步细化区间,确定后即为所求的单调区间.
解答:解:(1)∵f(x)为奇函数,
故f(x)的定义域关于原点对称
又f(x)的定义域为 (显然b≠0,否则f(x)为偶函数)
(显然b≠0,否则f(x)为偶函数)
∴ ,即c=0
,即c=0
于是得 ,且
,且 ,
,
∴
∴ 又b∈Z
又b∈Z
∴b=1
∴a=1
故a=b=1,c=0,符合f(x)在[1,+∞)上单调递增
(2)由(1)知 ,
,
 =
=
①当-1<x1<x2<0时,显然x1-x2<0,0<x1x2<1,x1x2-1<0
∴f(x1)-f(x2)>0
∴f(x)为减函数
②当x1<x2<-1时,显然x1-x2<0,x1x2>1,x1x2-1>0
∴f(x1)-f(x2)<0
∴f(x)为增函数
综上所述,f(x)在(-∞,-1]上是增函数,在[-1,0)上是减函数.
点评:本题主要考查函数利用奇偶性和函数值,单间性来求解析式,在研究单调性中分类讨论的思想应用.
(2)用单调性定义来探讨,先在给定的区间上任取两个变量,且界定大小,再作差变形,在与0比较中出现讨论,再进一步细化区间,确定后即为所求的单调区间.
解答:解:(1)∵f(x)为奇函数,
故f(x)的定义域关于原点对称
又f(x)的定义域为
 (显然b≠0,否则f(x)为偶函数)
(显然b≠0,否则f(x)为偶函数)∴
 ,即c=0
,即c=0于是得
 ,且
,且 ,
,
∴

∴
 又b∈Z
又b∈Z∴b=1
∴a=1
故a=b=1,c=0,符合f(x)在[1,+∞)上单调递增
(2)由(1)知
 ,
, =
=
①当-1<x1<x2<0时,显然x1-x2<0,0<x1x2<1,x1x2-1<0
∴f(x1)-f(x2)>0
∴f(x)为减函数
②当x1<x2<-1时,显然x1-x2<0,x1x2>1,x1x2-1>0
∴f(x1)-f(x2)<0
∴f(x)为增函数
综上所述,f(x)在(-∞,-1]上是增函数,在[-1,0)上是减函数.
点评:本题主要考查函数利用奇偶性和函数值,单间性来求解析式,在研究单调性中分类讨论的思想应用.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
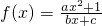 是奇函数,(a,b,c都是整数),且f(1)=2,f(2)<3,f(x)在[1,+∞)上单调递增.
是奇函数,(a,b,c都是整数),且f(1)=2,f(2)<3,f(x)在[1,+∞)上单调递增. 是奇函数,则a= 。
是奇函数,则a= 。