题目内容
已知双曲线P1(-2,
解:因为双曲线的焦点位置不确定,所以设双曲线方程为mx2+ny2=1(mn<0),因P1、P2在双曲线上,所以有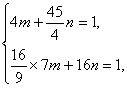 解得
解得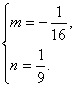
∴所求双曲线方程为![]() +
+![]() =1,即
=1,即![]() =1.
=1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
已知双曲线P1(-2,
解:因为双曲线的焦点位置不确定,所以设双曲线方程为mx2+ny2=1(mn<0),因P1、P2在双曲线上,所以有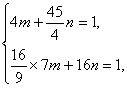 解得
解得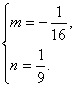
∴所求双曲线方程为![]() +
+![]() =1,即
=1,即![]() =1.
=1.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案